编译原理 课程笔记

第一章绪论

一到四章的概念也就图一乐，真学习还得看第五章

引言

语言

语言：一组规则的组合

字母表的定义
词法规则：单词符号的形成规则
语法规则：（短语、从句、句子、段落、文章）语法单位的形成规则
语义规则：单词符号和语法单位的含义规则
语用规则：语义规则的发展和延伸。在一定的语境中，单词和语法单位体现出来的具体意义，需要根据上下文进行明确

机器语言、汇编语言、高级语言

机器语言 -> 汇编语言 -> 高级语言

机器语言：由二进制指令组成。计算机可以直接执行
汇编语言：将机器语言符号化的结果
低级语言：与机器有关的语言（指令的操作码、指令格式、寻址方式、数据格式）
高级语言：和机器无关的语言

翻译

翻译：等价的变换

计算机只可直接执行用机器语言编写的程序。而用汇编语言和高级语言编写的程序，机器不能直接执行。必须将它们翻译成完全等价的机器语言程序才能执行。

翻译过程：

机器语言 <–汇编程序– 汇编语言 <–编译程序– 高级语言

实现：编写一个高级语言的编译程序的工作，通常称为对这个语言的实现

与编译有关的三种语言、三种程序：

源语言、宿主语言、目标语言
源程序、编译程序、目标程序
高级语言涉及的三类人：
设计者、实现者、使用者

解释

BASIC 是最简单的高级语言。BASIC 程序不是编译执行，而是对源程序进行解释（分析），直接计算出结果。
解释需要解释程序(解释器)
LISP，ML，Prolog 和 Smalltalk 均是解释型的语言。
Java 被当作一种解释型语言。翻译产生字节码的中间代码，可以在 Java 虚拟机上运行。

解释执行特别适合于动态语言和交互式环境，便于人机对话。
重复执行的语句需要重复翻译，比编译执行要花去更多的时间，执行效率较低。

强制式语言、函数式语言、逻辑式语言、对象式语言

程序设计语言按设计的理论基础分为四类语言:

强制式语言:基础是冯·诺依曼模型
函数式语言:基础是数学函数(函数运算)
逻辑式语言:基础是数理逻辑、谓词演算
对象式语言:基础是抽象数据类型

绑定

实体：程序的组成部分，如变量，表达式、程序单元等
属性：实体具有的特性
绑定：实体与其各种属性建立起联系的过程称为绑定（约束）
**描述符(表)**：描述实体属性的表格

静态和动态

静态特性：编译时能确定的特性
动态特性：运行时才能确定的特性

静态绑定：绑定在编译时完成，且在运行时不会改变。
动态绑定：绑定在运行时完成。

静态作用域绑定:按照程序的结构定义变量的作用域（C语言等）。依据定义变量的位置进行确定。
动态作用域绑定:按照过程的调用关系动态地定义变量的作用域（SNOBL4 语言等）

变量的四个属性

作用域：全局变量、局部变量、非局部变量
生存期
值
类型

快进到第四章

第二章数据类型

略

第三章控制结构

略

第四章程序语言的设计

前言

语言 = 语法 + 语义

描述语法的方法：文法 or 语法图

文法和语法图是语言语法的等价表示。

文法：

<标识符>→<字母>
<标识符>→<标识符><字母>
<标识符>→<标识符><数字>
<字母>→A|…|Z|a|…|z
<数字>→0|…|9

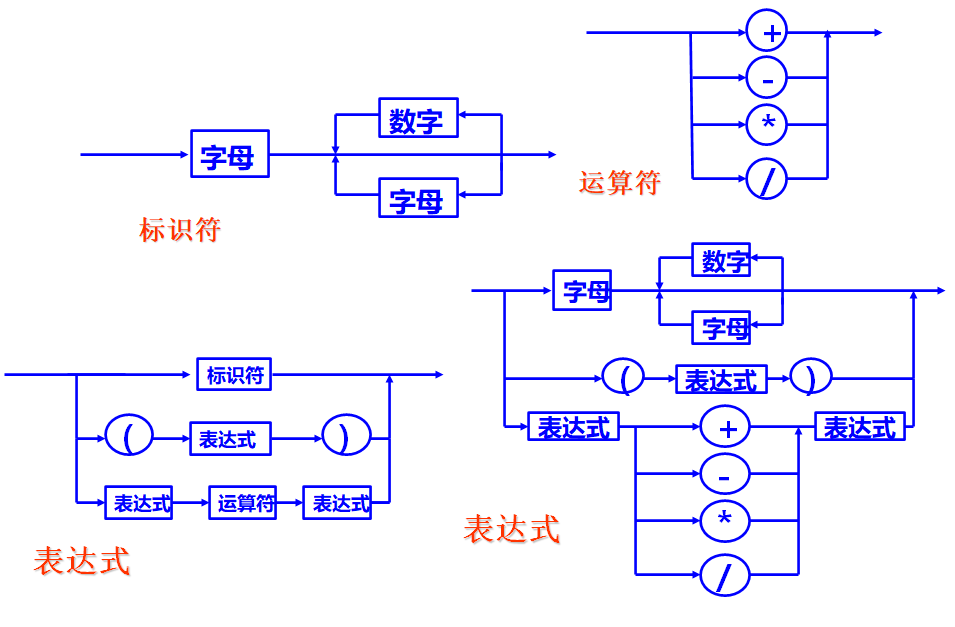
描述语义的方法：许多语言仍采用自然语言描述语义。

文法

文法的形式定义

文法的形式定义： $G = (V_T, V_N, S, P)$

$V_T$ 为终结符的非空有限集；
$V_N$ 为非终结符的非空有限集；
$V=V_T \bigcup V_N$
$S$ 是文法的开始符号，有 $S\in V_N$ ；
$P$ 为产生式 $\alpha\to\beta$ 的非空有限集，其中：
$\alpha$ 和 $\beta$ 是由终结符、非终结符组成的串，且 $\alpha$ 至少应含有一个非终结符。即 $\alpha=V^*V_NV^*, \beta=V^*$
$^*$ 表示前面的符号重复零次或多次（这很正则表达式）

G: Grammar
T: Terminal Symbols
N: Non-Terminal Symbols
S: Start Symbol
P: Production

产生式的简化

$$\left.\begin{aligned}
\alpha&\to\beta_1 \\
\alpha&\to\beta_2 \\
&…\\
\alpha&\to\beta_n
\end{aligned}\right\}
\alpha\to\beta_1|\beta_2|\beta_n
$$

$\beta_1, \beta_2, \beta_n$ 称为 $\alpha$ 的候选式。

文法的表示

描述文法，直接给出产生式集合 (P) 即可。

$$\begin{aligned}
E &→ E+T | E-T | T \\
T &→ T*F | T/F | F \\
F &→ (E) | i
\end{aligned}$$

文法的分类

分为 0 型文法、1 型文法、2 型文法、3 型文法。数字越大，规定越严格，越规范。

文法	（在上一级基础上增加）限制	中文
0型文法(PSG)	$\alpha\to\beta$	无限制
1型文法(上下文有关文法CSG)	$α$ 长度小于 $β$ 长度（$S→ε$例外）	右边的表达式长于左边
2型文法(上下文无关文法CFG)	$A→β$	左边是独立的非标识符
3型文法(正则文法RG,或右线性文法RLG)	$A→u$或$A→wB$, $u\in V_T^*, w\in V_T^+$	右边不以非标识符开头

推导的表示

直接推导（由产生式右边替换产生式左边）： $wαγ\Rightarrow wβγ$
任意步推导（0 步或多步）：$y \Rightarrow^* z$
多步推导（1 步或多步）：$y \Rightarrow^+ z$

最右推导：总是展开最右边的非终结符

句型、句子、语言

$G = (V_T, V_N, S, P)$

句型：S 能推导出的 $w$
句子：S 能推导出的只含终结符的 $w$
语言：G 产生的所有句子的集合 $L(G)=\{α│S\Rightarrow^+α 且 α\in V_T^*\}$

例 4 有点难。

文法等价

两个文法 $G$ 和 $G’$，如果有 $L(G)=L(G’)$，则称 $G$ 和 $G’$ 等价

推导树

对于文法 $E→E+E|E*E|(E)|i$，句子 $i+i*i$，其两棵推导树：

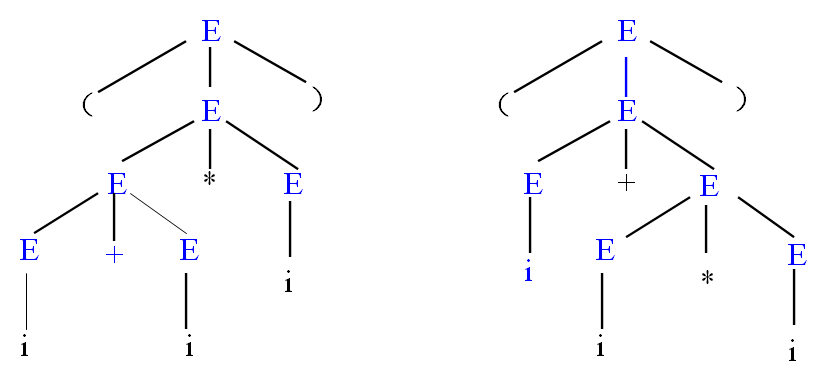
文法的二义性：一个句子有两棵不同的推导树。

第五章编译

复习概念

源语言、宿主语言、目标语言
源程序、编译程序、目标程序

自驻留：若编译程序生成宿主机执行的机器代码，称为自驻留的编译程序
自编译：若编译程序是用源语言编写的，则为自编译的编译程序
交叉编译：若编译程序生成的不是宿主机(别的机器)执行的机器代码，称为交叉编译

编译步骤

逻辑上：

源程序的分析
目标程序的合成

具体：

词法分析
语法分析
语义分析与中间代码生成
中间代码优化
目标代码生成

编译的每个步骤都需要进行符号表管理和出错处理。

词法分析

分析输入字符串
根据词法规则识别出单词符号：基本字、标识符、字面常量、运算符和界符

语法分析

根据语法规则，识别各类语法单位：表达式、语句、程序单元和程序
进行语法检查

语义分析与中间代码生成

根据语义规则，对语法正确的语法单位进行翻译
可以直接生成目标程序
但目标程序的执行效率低
因此，生成中间代码

中间代码：

大多数编译器采用中间代码来描述源程序的语义。
这种中间语言对应某种抽象机
结构简单，语义明确，易于翻译成目标代码，同时也便于优化和移植。

优化

对中间代码进行等价变换，提高代码的时空效率。
语义分析产生的中间代码不依赖于实际机器，易于实现一些等价变换，使生成的目标程序占用空间更少，执行更快。

目标代码生成

根据优化后的中间代码及有关信息，可生成较为有效的目标代码：
目标机的机器语言程序或汇编语言程序
若生成的是汇编语言程序，还需由将其汇编成机器语言程序。

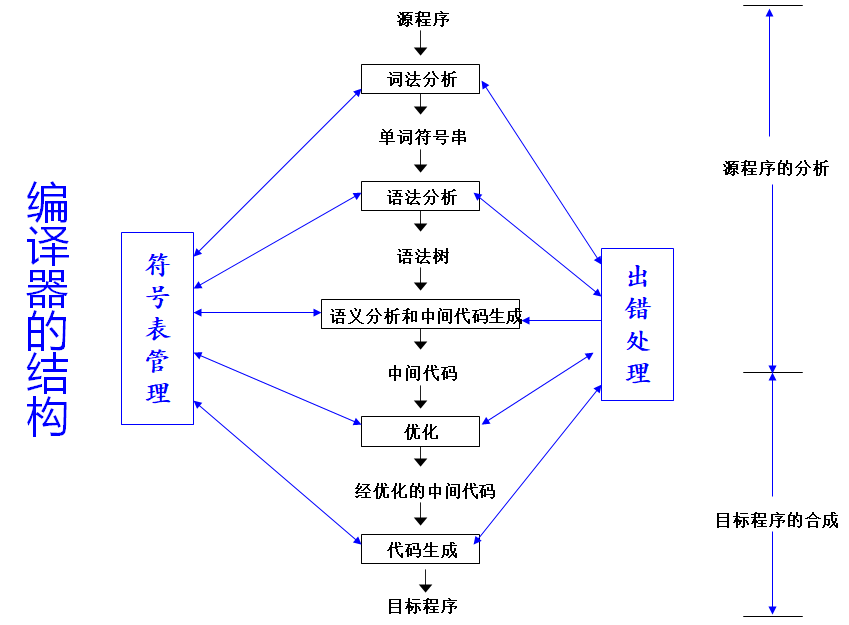
完整的程序处理过程

从分析源程序到建立一个可执行的目标程序，处理过程还需要其它工具程序的配合：

预处理器
汇编器
连接器
装入器

编译前端和后端

在现代编译器中，通常将编译过程划分为前端和后端两大部分，分别加以实现。
前端和后端通过中间代码连接，可极大的提高编译器设计与实现的效率。
前端：主要是与源程序相关的部分，包括词法、语法分析、语义分析和中间代码生成等。
后端：主要是与目标程序相关的部分，包括优化、目标代码生成等。

第六章词法分析

从这里才开始变难。

概述

词法分析：扫描源程序的字符串,按照词法规则,识别出单词符号作为输出；对识别过程中发现的词法错误(非法的字符、不正确常量、程序括号等) 进行处理。

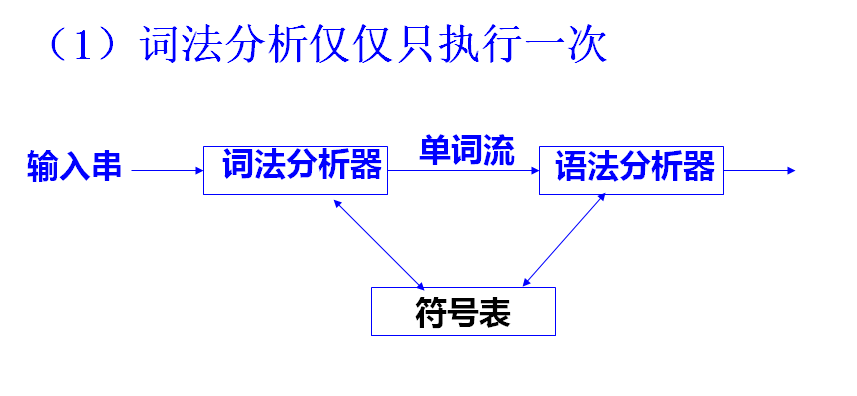
单词的种类

标识符
关键字
常量
运算符
分界符

while(*pointer!='\0') pointer++;

while       关键字   	 
(           界符	 
*           运算符 	 
pointer     标识符   	 
!=          运算符	 
'\0'        常量     	 
)	        界符	 
pointer     标识符
++          运算符   	 
;           界符	 
'\n'        界符

单词的输出形式

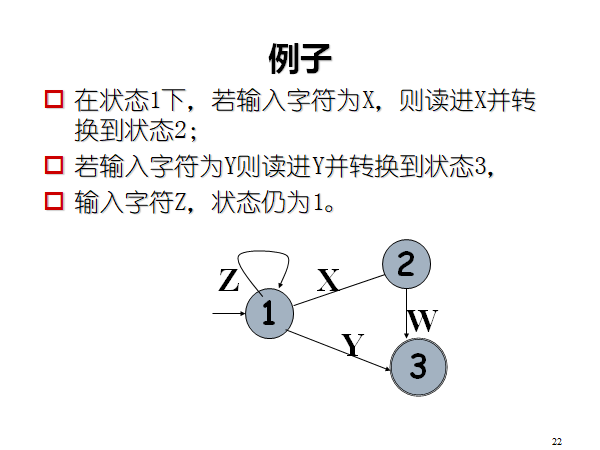
采用二元式：(单词类别，单词)

单词类别：区分单词所属的类(整数编码)
单词：单词的属性值

单词类别的划分

单词的编码随类别不同而不同。
基本字、运算符、界符的数目是确定的，一字一码，它的第二元可以空缺。

标识符通归一类。
常量可按整型、实型、字符型、布尔型等分类。
常量或标识符将由第二元—-单词的属性值来区别：
- 通常将常数在常量表中的位置（编号）作为常量的属性值；
- 将标识符在符号表中的位置（编号）作为标识符的属性值。

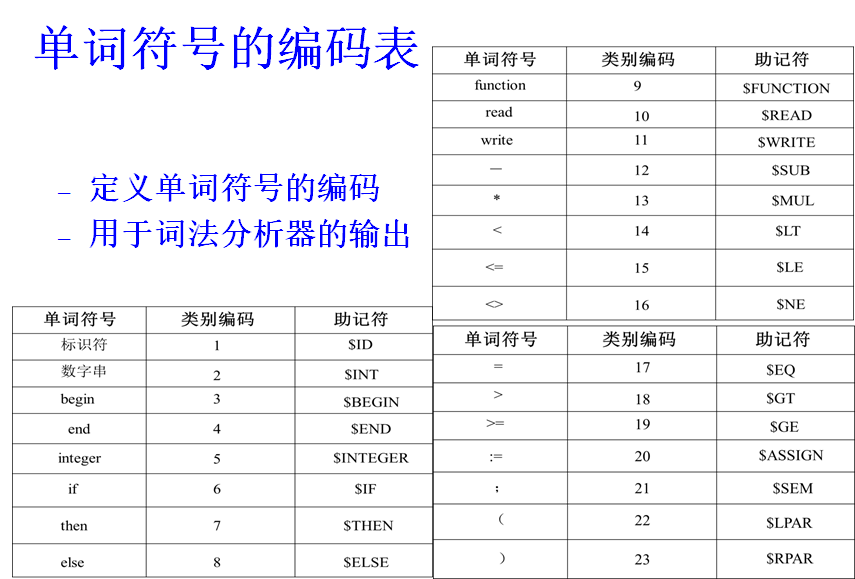
状态转换图

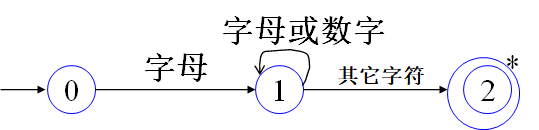
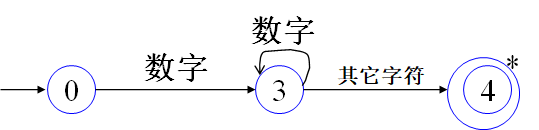
词法分析器的转换图

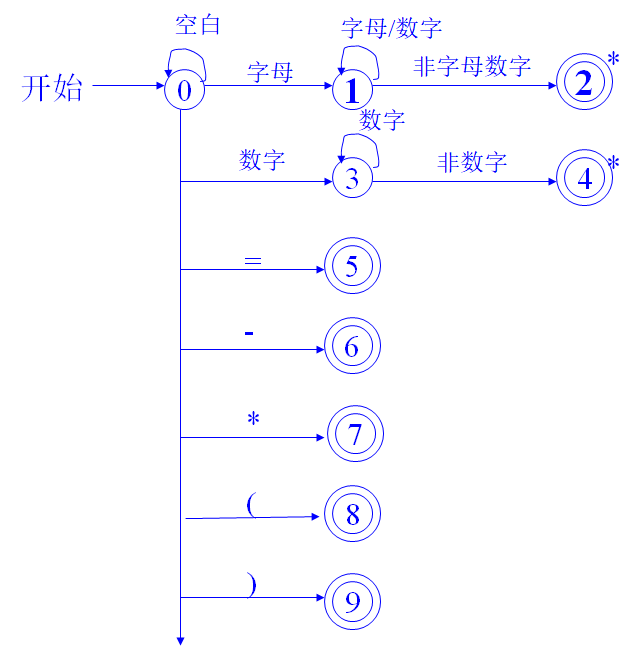
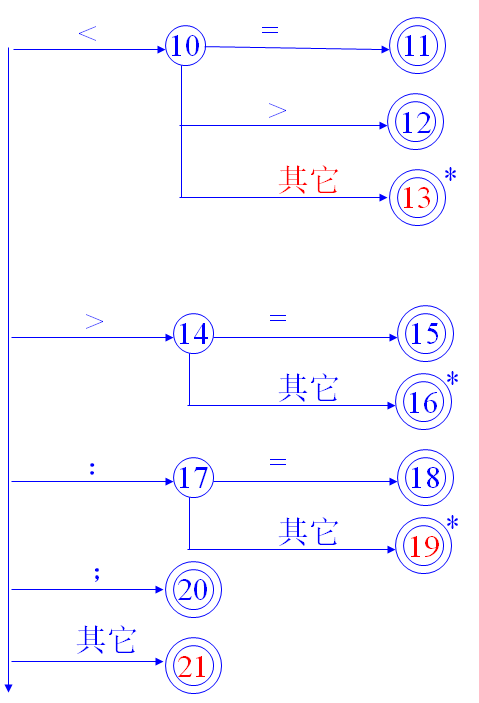
词法分析器

略，看 PPT 吧

第七章自上而下的语法分析

编译理论中，语法分析是对高级语言的语法单位的结构进行分析。
语法单位结构可以用上下文无关文法来描述。
下推自动机可用于识别上下文无关文法所描述的语法单位。
上下文无关文法及下推自动机是语法分析的理论基础。

语法分析：对无关文法 $G = (V_T, V_N, S, P)$ 及符号串 $w$，判断 $w$ 是否是文法 $G$ 的一个合法句子，即：
$$S\Rightarrow^*w$$

引言

语法分析的方法通常有两类：

自上而下(自顶向下)的分析方法（第七章）：从 $S$ 出发，能否找到一个最左推导序列，使得 $S\Rightarrow^*w$；或者从根结点 $S$ 开始，能否构造一棵语法树，使得该语法树的叶结点自左至右的连接正好是 $w$。
自下而上(自底向上)的分析方法（第八章）：从 $w$ 出发，能否找到一个最左规约（最右推导的逆过程）序列，逐步进行规约，直至文法的开始符号 $S$。

自上而下的语法分析可分为不确定和确定的两类。

回溯分析法是不确定的分析方法。
递归下降分析法和预测分析法属于确定的分析方法。

回溯分析法

其实就是 DFS。

实例：

$$\begin{aligned}
S&→xAy \\
A&→ab│a
\end{aligned}$$

输入串为 $xay$。

回溯分析的动画过程看 PPT。

采取试探的方法来分析每一个候选式，分析的过程很可能产生回溯。
可能产生回溯的原因有： (1)公共左因子 (2)左递归 (3)$ε$ 产生式

公共左因子

公共左因子，是指在文法的产生式集合中，某个非终结符的多个候选式具有相同的前缀。

$$A→αβ_1│αβ_2$$

若所有候选式都没有公共左因子，就可以选择惟一匹配的候选式，减少不必要的回溯

左递归

左递归：$A\Rightarrow^+Aβ$
直接左递归：$A\Rightarrow Aβ$

回溯分析法特点

回溯分析法是一种不确定的方法：使用试探的方法穷举每一种可能，当分析不成功时，则回退到适当位置再重新试探其余可能的推导。穷尽所有可能的推导，仍不成功，才能确认输入串不是该文法的句子。

主要缺陷

选择候选式进行推导是盲目的
若文法存在左递归，语法分析还可能产生无限递归
引起时间和空间的大量消耗
无法指出语法错误的确切位置

针对产生回溯的原因，提出消除回溯的方法：引进确定的语法分析方法——递归下降分析法和预测分析法。

为了消除回溯，对任何一个非终结符和当前的待匹配符号，期望

要么只有一个候选式可用
要么没有候选式可用

递归下降分析法

方法步骤

提取公共左因子（看 PPT）
消除左递归

消除直接左递归（改写为右递归）
间接左递归（$A\Rightarrow^+Aα$）的消除利用算法进行
a. 将文法 $G$ 的所有非终结符按任一给定的顺序排列为 $A_1，A_2，…，A_n$
b. 消除可能的左递归（算法见后）
c. 化简：删除多余产生式

// 消除左递归
for i:=1 to n do
  for j:=1 to i-1 do
    把形如Ai→Ajα的产生式改写为
      Ai→δ1α|δ2α|...|δkα
    消除Ai产生式可能的直接左递归

消除例子中的左递归：

$$\begin{aligned}
S&→Qc│c \\
Q&→Rb│b \\
R&→Sa│a \\
\end{aligned}$$

递归下降分析器的构造

在文法 G 中，如果

没有任何公共左因子
没有任何左递归
则有可能构造出不带回溯的分析程序

预测分析法

构造 First 集

A -> aB，A 就有 {a}
A -> B，A 可以把 B 的复制过来
A -> BC，若 B 可以为 ε，A 就还能复制 C 的

构造 Follow 集

FIRSTVT
E + ( * i
T * ( i
F ( i

第八章自下而上语法分析

概念

短语：某个祖先的所有没孩子的子孙组成的语句
直接短语：某个没有孙子的爸爸的孩子组成的语句
句柄：最左直接短语
素短语：短语至少有一个终结符，且不不含更小的素短语（若 i 是素短语，则 Fi* 不是素短语）

算符优先分析法

构造 FIRSTVT 集

A -> aBc 或 A -> Bac，A 就有 {a}
A -> BC，A 可以把 B 的复制过来
A -> BC，若 B 可以为 ε，A 就还能复制 C 的

构造 LASTVT 集

A -> caB 或 A -> cBa，A 就有 {a}
A -> BC，A 可以把 C 的复制过来
A -> BC，若 C 可以为 ε，A 就还能复制 B 的

算符优先关系表

优先：先归约的符号被称为优先级高。
先看行，再看列。如 + 行 i 列为 >，则 + > i。
规则：若 E+T，则 LASTVT(E) > +，+ < FIRSTVT(T)。
- 还要添加 #S# 这个文法
- 这里的大于、小于没有对称性（a>b 不能推出 b<a）
- 推荐先填等号，再按行填小于，再按列填大于

LR 分析法

第九章语义分析

符号表

符号表：

名字 | 信息

常用的符号表结构：线性表、Hash 表

语义分析概论

语义分析的主要工作

语义分析 = 静态语义检查 + 语义处理

静态语义检查：
(1) 类型检查：数据的使用应与类型匹配
(2) 控制流检查：用以保证控制语句有合法的转向点:
如不允许goto语句转入case语句流; break语句需要在switch或循环语句.
(3) 一致性检查：如数组维数是否正确; 变量是否已经定义；变量是否重名；case常量不能相同等。

语义处理：
说明语句: 登记信息；
执行语句：生成中间代码。

语法制导翻译

为每个产生式配上一个语义子程序

在语法分析过程中，根据每个产生式对应的语义子程序（语义动作）进行翻译（生成中间代码）的方法称为语法制导翻译。

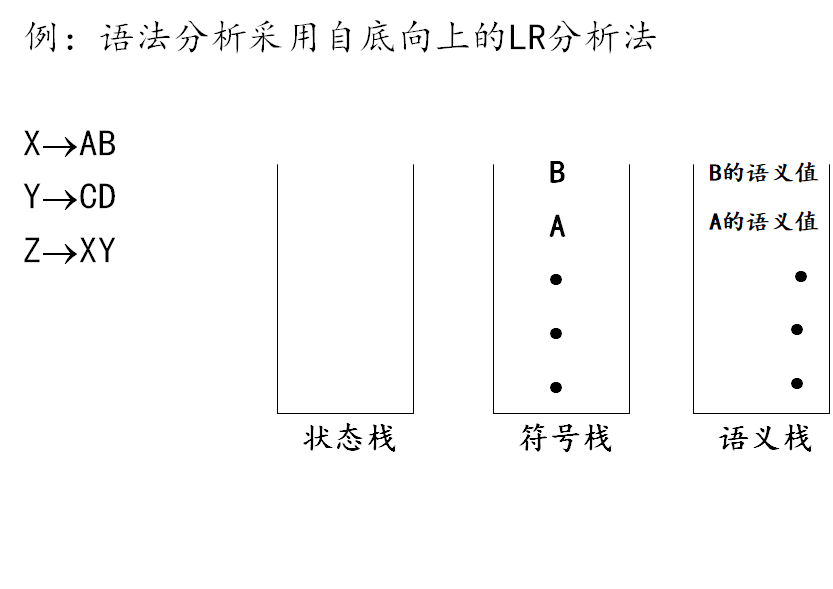
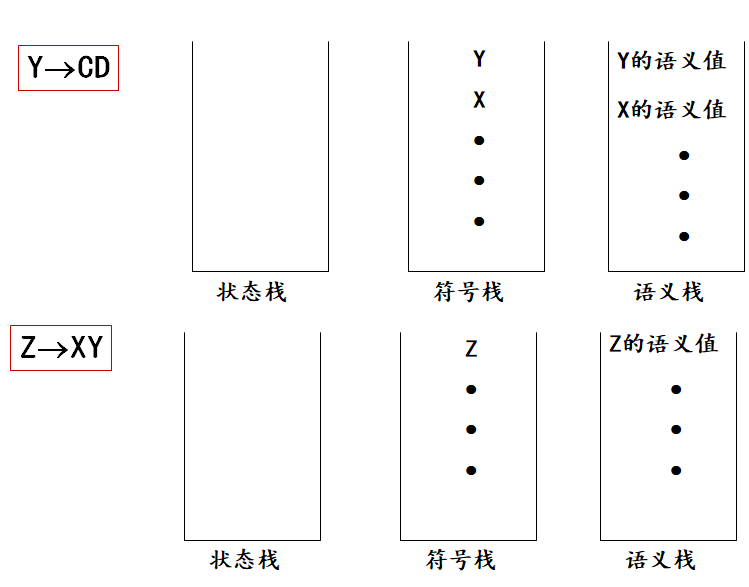
语义值

在描述语义动作时，需要赋予每个文法符号以各种不同的“值”，这些值统称为“语义值”.如，“类型”，“种属”，“地址”或“代码”等。通常用X.TYPE,X.CAT,X.VAL来表示这些值。

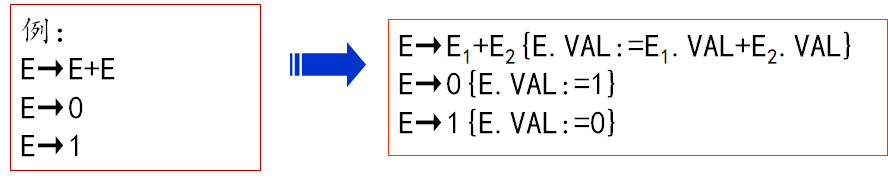
中间代码

中间代码一种与具体机器无关的抽象代码，有多种形式。四元式形式: (op,ARG1,ARG2,RESULT)

op—运算符
ARG1—第一运算量
ARG2—第二运算量
RESULT—结果

如: A:=（-B）*(C+D) 翻译成

(@,B,_,t1)
(+,C,D,t2)
(*,t1,t2,t3)
(:=,t3,_,A)

四元式出现顺序和表达式计值顺序一致;四元式之间的联系通过临时变量来实现。

简单赋值语法分析的翻译

语义变量及过程

X.a：文法符X相应属性a,如i.name,E.place。E.place:表示E所代表的变量在符号表的入口地址。
newtemp：语义函数，每调用一次产生一个新的临时变量。
entry(i)：语义函数，查符号表，返回变量i的入口。
IP：指令指针，初始化为0，也可以是指定的初值。
gen(OP,ARG1,ARG2,RESULT)：语义过程，生成一个四元式(OP,ARG1,ARG2,RESULT),并填入四元式表中。同时 ip:=ip+1

翻译方案

1 2	A → i:=E E → E1 op E2 \| -E1 \|(E1)\| i

A→i:=E
{
    P=entry(i.NAME);
    If(P!=0) 
        gen ( :=, E.place, _, P)
    Else error();
}

E→E1 op E2
{
    E.place:=newtemp;
    gen(op,E1.place,E2.place,E.place)
}

E →-E1 
{
    E.place:=newtemp; 
    gen(@,E1.place,_,E.place)
}

E →(E1)
{  E.place:= E1.place  }

E →i  
{  P=entry(i.NAME);
  If(P!=0)  E.place:=P
  Else error();

类型转换

对表达式E增加类型属性E.type;
引进类型转换指令 (itr,x,_,t)

t:=newtemp;
if E1.type=integer 
   and E2.type=integer 
then begin
  gen(opi,E1.place,E2,place,t);
  E.type:=integer
  end

else if E1.type=real and E2.type=real 
then begin 
  gen(opr,E1.place,E2.place,t);
  E.type:=real  
  end

else if E1.type=integer then
  begin t1:=newtemp;
    gen(itr,E1.place,_,t1);
    gen(opr,t1,E2.place,t);
    E.type:=real
  end

else begin t1:=newtemp;
  gen(itr,E2.place,_,t1);
  gen(opr,E1.place,t1,t);
  E.type:=real
end;

E.place:=t;

说明语句的翻译

不产生可执行指令
仅负责填表：将被说明对象的类型及相对存储位置记入各自的符号表中

文法

1 2	D→D;D│i:T T→real│integer│array[num] of T1│↑T1

语义变量和过程

负责填下面两个东西！

(1)offset:相对位移量,初值为0,是一个全局变量
(2)T.type:数据类型
(3)T.width:数据宽度
(4)enter:语义过程,将变量名及其类型和相对存储位置记入符号表中。

翻译方案

S →MD
M →ε        { offset:=0 }
D → D1;D2
D →i:T      { enter(i.name,T.type,offset); offset := offset+T.width }
T→integer {  T.type:=integer;  T.width:=4  }

控制语句的翻译

布尔表达式的翻译

文法

B→i
B→i1 rop i2

（1）if  B  then  S
（2）if  B  then  S else S
（3）while B do S

语义变量

B.T：真出口，记录B为真的转移语句的地址；
B.F：假出口，记录B为假的转移语句的地址。

转移语句的四元式

1
2
3

(jrop,P1,P2,0) 
(jnz,P1,-,0)
(j,-,-,0)

0 是转移地址，从上往下分析的时候可能不知道要转义到哪里，所以会挖坑，后面会填坑。

翻译方案

B→i
{
    B.T:=ip;
    gen(jnz,entry(i),-,0);
    B.F:=ip;
    gen(j,-,-,0)
}

B→i1 rop i2
{
    B.T:=ip;
    gen(jrop,entry(i1),entry(i2),0);
    B.F:=ip;
    gen(j,-,-,0)
}

无条件转移语句翻译

goto L，L 已经定义

…
L: ...   /*此时，将L登记入符号表*/
…
goto L;  /*查表，发现L已定义，生成四元式*/

goto L，L 未定义

…
goto L; /*将L记入符号表，定义否标记为“否”，
         地址栏写当前IP，生产无条件转移 */
…
goto L; /*拉链，即生成向上指的链表*/
…
L: …   /*定义否标记改为“是”，回填，即根据链表依次改写跳转的地址栏*/
…

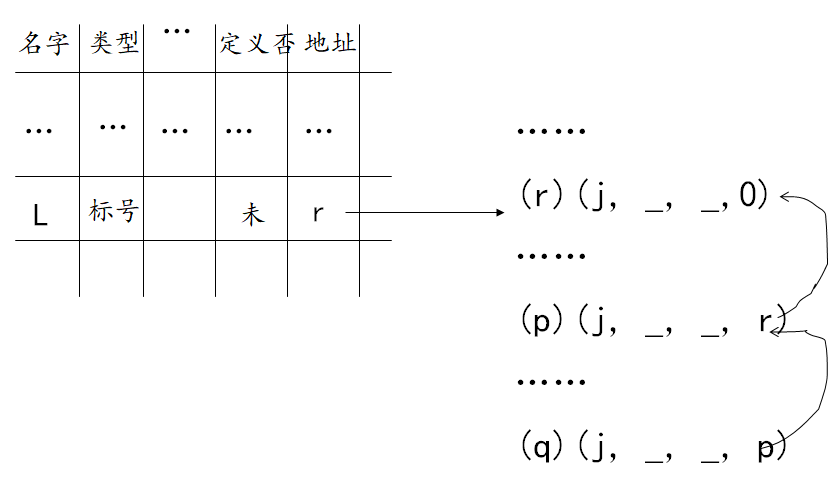
标号语句的处理方法

文法：

label →i:

i（假定为L）不在符号表中：则把它填入，置“类型”栏为“标号”，“定义否”栏为“已”，“地址”栏为ip的当前值；
若L已在符号表中，“类型” 为“标号”, “定义否”栏为“否” :把“定义否”改为“已”，然后把“地址栏”中的链首q取出，同时把ip当前值填入其中，最后执行 backpatch（q，ip）语义过程进行回填
若L已在符号表中，但“类型”不为“标号”,或“定义否” 为“已”：则“名字重定义”

backpatch（q，ip）为语义过程：把q为链首的链上所有四元式的第四区段都填为ip

If 条件语句的翻译

文法

1	S→if B then S1 │ if B then S1 else S2

if B then S1：S1的第一条四元式
用以“回填”
if B then S1 else S2：S1、S2的第一条四元式用以“回填”

(1)B具有真假出口
B为真假时的转向不同
在翻译B时其真假出口有待“回填”
(2)因if语句的嵌套,必须记录不确定转移目标的四元式的地址—拉链技术

语义变量及过程

N.CHAIN：记录不确定转移目标的四元式形成的，不确定 label 地址时就调用这个；一般来说，N.CHAIN 的含义是 N 结束以后要跳的位置
merge(t1,t2): 语义函数，合并链表，返回合并后的链头t2，用于合并链表/拉链
backpatch(t1,code): 语义过程，用code回填t1，确定 label 地址时就调用这个

如:

(p) (j, -, -, 0)     (u) (j, -, -, 0)
    ……                     ……
(q) (j, -, -, p)     (v) (j, -, -, u)
    ……                     ……
(r) (j, -, -, q)     (w) (j, -, -, v)
t1=r                   t2=w

执行merge(t1,t2)后

(p) (j, -, -, 0)    (u) (j, -, -, r)
    ……                 ……
(q) (j, -, -, p)    (v) (j, -, -, u)
    ……                 ……
(r) (j, -, -, q)    (w) (j, -, -, v)

链头t2=w

执行backpatch(t2,120)后

(p) (j, -, -, 120)  (u) (j, -, -, 120)
    ……                   ……
(q) (j, -, -, 120)  (v) (j, -, -, 120)
    ……                   ……
(r) (j, -, -, 120)  (w) (j, -, -, 120)

翻译方案

if-then 不负责生成四元式，只负责填 0！！！

S→if B then S1
S→M S1
M→if B then

M→if B then
{
    backpatch(B.T, ip); // B.T 即为下一句的地址，所以可以直接填当前 ip
    M.CHAIN:=B.F        // B.F 在后面，所以创建链表
}

/*
 * 另外,在图9-3中，整个语句翻译完成后,B.F仍不能确定,只能
 * 将它作为S的语义值S. CHAIN暂时保留下来。如果S,本身也是控
 * 制语句(比如另一个嵌套的条件语句),它也有语义值S. CHAIN未
 * 确定,则B.F和S.CHAIN应转到同一个地方,因此要将它们链
 * 接起来,组成一个新的链,链首地址记录在S的语义值S. CHAIN
 * 中,这项工作由语义函数merge()完成。
 */
S→M S1
{
    S.CHAIN:=merge(M.CHAIN, S1.CHAIN)   // B.F
}

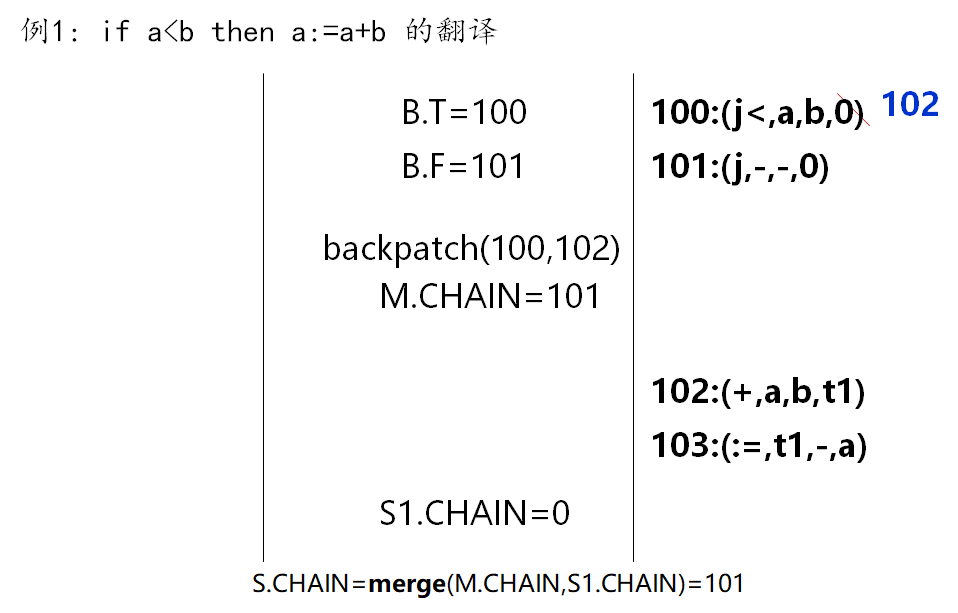
这里还有一个 bug：S 执行完以后还没有回填 S.CHAIN。这一步其实是交给 S 后面的分号来做的，而这是执行语句的文法，已经脱离了本节讨论的控制语句文法。因此上面的例子（以及后面的例子）并没有提及。

if-then-else 只需要生成一个四元式：then 后的语句执行完以后要 jump 到 else 后

S→if B then S1 else S2 
M→if B then
N→M S1 else
S→N S2

M→if B then
{
    backpatch(B.T, ip);
    M.CHAIN:=B.F
}

N→M S1 else
{
    q:=ip;
    gen(j,-,-,0);
    backpatch(M.CHAIN,ip);
    N.CHAIN:=merge(S1.CHAIN , q)
}

S→N S2
{
    S.CHAIN:=merge(N.CHAIN, S2.CHAIN)
}

While 语句的翻译

文法

1	S→while B do S1

翻译方案

while 语句其实就是 if-then 语句多了一个 jump

W→while
D→W B do
S→D S1

W→while
{
    W.code := ip;
}

D→W B do
{
    backpatch(B.T, ip);
    D.CHAIN = B.F;
    D.code = W.code;    // 子变量值传给父变量
}

S→D S1
{
    backpatch(S1.CHAIN,D.code);
    gen(j,-,-,D.code);
    S.CHAIN:=D.CHAIN;
}

可以看出,许多语句的最后都有一个S.CHAIN链,然而对赋值语句来说,没有需要返填的三地址语句,为了统一，我们给赋值语句赋一个空链。语义程序如下:

1 2	S->A {S.CHAIN=0;}

For 循环语句的翻译

文法

1	S→for i:=1 to N do S1

其语义为：

        i:=1;
again:  if i<=N then begin
            S1;
            i:=i+1;
            goto again
        end

代码结构可为：

F+0:（:=，'1'，-，i）
F+1: (j<=,i,N,F+3)
F+2: (j,-,-,0)
F+3: (S1的四元式序列)
...
D+0: (+,i, ‘1’,i)
D+1: (j,-,-,F+1)

语义变量

为了在生成S1的代码之前生成i:=1等三个语句,必须改写文法。

1 2	F→for i:=1 to N do S→F S1

F.again:记录F+1
F.CHAIN:记录前述F+2的地址
F.place:记录i在符号表入口

翻译方案

F→for i:=1 to N do
{
    gen(:=,'1',-,entry(i));
    F.again:=ip;
    gen(j<=,entry(i),N,F.again+2);
    F.CHAIN:=ip;
    gen(j,-,-,0);
    F.place:=entry(i)
}

S→F S1
{
    backpatch(S1.CHAIN,ip);
    gen(+,F.place,'1',F.place);
    gen(j,-,-,F.again);
    S.CHAIN:=F.CHAIN
}

另一道例题：写出下面代码的中间代码序列。

1	for i=1 to 10 do if A>100 then C=C+1;

100: (=, 1, -, i)
101: (J<=, i, 10, 103)    F.again=103
102: (J, -, -, 109)
103: (J>, A, 100, 105)
104: (J, -, -, 107)
105: (+, C, 1, t1)
106: (=, t1, -, C)
107: (+, i, 1, i)
108: (J, -, -, 103)
109:

更多例题：

1	if (A<X) & (B>0) then while C>0 do C:=C+D;


100 (j<， A， X， 102)
101 (j， -， -，  109)
102 (j>， B， 0， 104)
103 (j， -， -，  109)
104 (j>， C， 0， 106)
105 (j， -， -，  109)
106 (+， C， D，   T1)
107 (:=， T1， -， C)
108 (j， -， -，  104)
109

z := 3;
while j< 10 do 
begin  
   j := x+1;
   if x <10 then  
           y:= A+m;
     	else  
           y:= A-m;
end

100 (=, 3, _, z)
101 (J<, j, 10, 103)
102 (J, -, -, 113)
103 (+, x, 1, t1)
104 (=, t1, -, j)
105 (J<, x, 10, 107)
106 (J, -, -, 110)
107 (+, A, m, t2)
108 (=, t2, -, y)
109 (J, -, -, 112)
110 (-, A, m, t3)
111 (=, t3, -, y)
112 (J, -, -, 101)

过程的的翻译（自学）

第十章代码优化和目标代码生成

优化是一种等价的，有效的程序变换
等价——不改变程序运行结果
有效——时空效率要高

优化按阶段分类：

源程序阶段的优化：优化数据结构和算法
编译优化：中间代码和目标代码优化

中间代码优化：便于移植（与机器无关）。又分为：

局部优化：在基本块内的优化
全局优化：超越基本块，基本块之间的优化

局部优化

划分基本块

(1)寻找入口语句

程序的第一条语句
由转向语句转移到的语句
紧跟在条件转向语句后的那个语句
(2)寻找出口语句
转向语句
停止语句
(3)基本块为：
每个入口地址（含）到下一个入口地址（不含）
每个入口地址（含）到下一个出口地址（含）
(4)不在任何基本块中的代码可以被删除

构造流图

下面是正确的废话：

$$G = (N, E, n_0)$$
(1)基本块集即为结点集N;
(2)包含程序第一个语句的基本块，为首结点n0;
(3)设基本块 Bi , Bj ∈ N ，若满足下列条件之一，则Bi ->Bj

Bj 紧跟在 Bi 之后，且 Bi 的出口语句不是无条件转向或停止语句
Bi 的出口语句为转向语句，其转向点恰为Bj 的入口语句

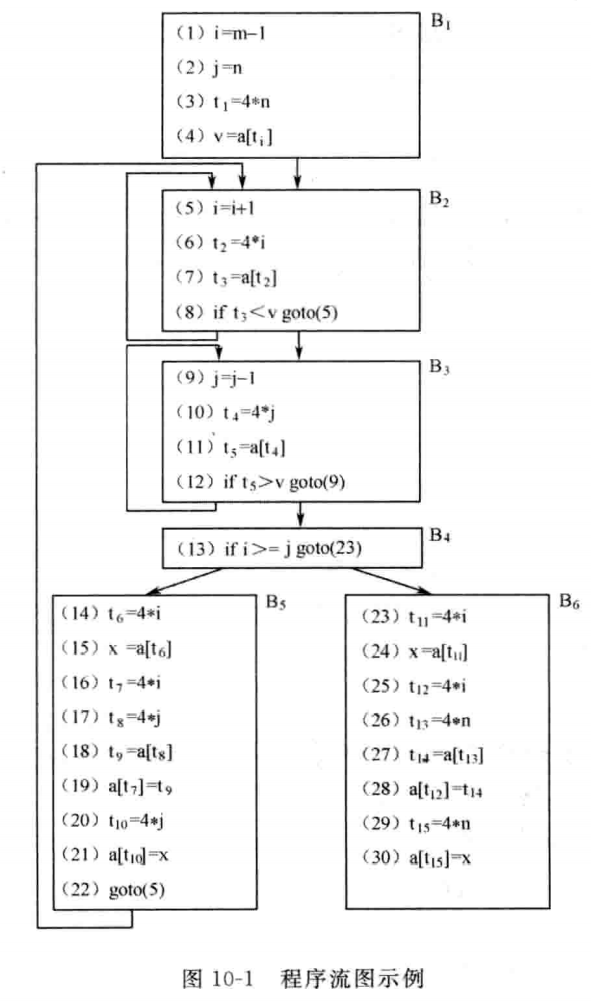
基本块内的优化

合并已知量

// 优化前
B := 1
C := 2
A := B + C

// 优化后
A := 3

删除公共子表达式

// 优化前
B := 1
C := 2
A := B + C
D := B + C

// 优化后
D := A

删除无用赋值

// 优化前
A := 1
A := 2

// 优化后
A :=2

删除死代码

若某个基本块实际不可能被执行，该基本块为死代码，可以删除。

例题

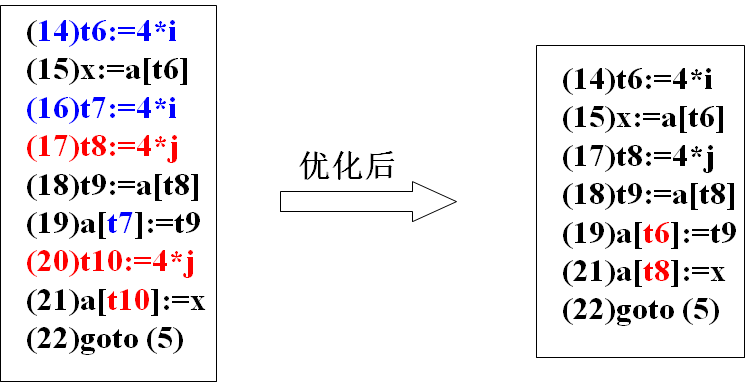
全局优化（自学）

本节只讨论对循环进行的优化。

循环的定义

循环：程序流图中，有唯一入口结点的强连通子图。

强连通子图：子图里面任意两个结点可以互通。

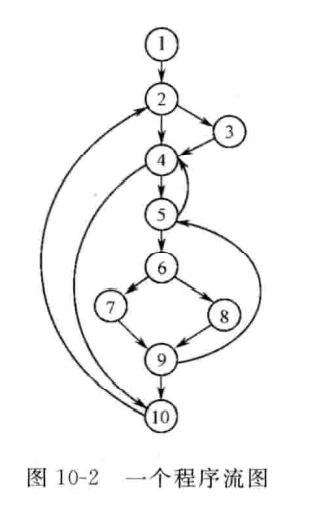
{5, 6, 7, 8, 9} 是循环：所有点都互通，且 5 是唯一入口。

循环的查找

必经结点：从流图的首结点出发，到达结点n的任一通路都必须经过的结点d，称为n的必经结点。记为 d DOM n

每个结点是它本身的必经结点，即n DOM n
首结点是任一结点的必经结点，即n0 DOM n

上图的必经节点集：

D(1)={1}
D(2)={1,2}
D(3)={1,2,3}
D(4)={1,2,4}
D(5)={1,2,4,5}
D(6)={1,2,4,5,6}
D(7)={1,2,4,5,6,7}
D(8)={1,2,4,5,6,8}
D(9)={1,2,4,5,6,9}
D(10)={1,2,4,10}

回边：若 d 是 n 必经节点，且存在边 n->d，则该边为回边。

上图有三条回边：

1
2
3

5->4
9->5
10->2

若 n->d 是回边，则图里能到n且不经过d的点的集合+n+d 就是由 n->d 组成的循环

上图的循环有：

1
2
3

5->4 组成 {5, 4, 6, 7, 8, 9}
9->5 组成 {9, 5, 6, 7, 8}
10->2 组成 {10, 2, 3, 4, 5, 6, 7, 8, 9}

循环优化方法

代码外提

// 优化前
for (int i = 0; i < n; i++)
{
    float pi = acos(-1);
    // ...
}

// 优化后
float pi = acos(-1);
for (int i = 0; i < n; i++)
{
    // ...
}

强度削弱

// 优化前
for (int i = 1; i < 10; i++)
{
    int j = i * 10 + 5;
}

// 把乘法优化成加法后
int j = 5;
for (int i = 1; i < 10; i++)
{
    j += 10;
}

例子中，i=循环次数+c 叫做基本归纳变量；j=循环次数*c1+c2 叫做同族归纳变量。强度削弱把基本归纳变量变为同族归纳变量，将乘法变为加法，还可以将普通加法变为变址器加法。

删除归纳变量

即改用同族归纳变量作为判断条件

// 优化前
int j = 5;
for (int i = 1; i < 10; i++)
{
    j += 10;
}

// 优化后
int j = 5;
for (; j < 5 + 10*10;)
{
    j += 10;
}

例题

优化前：

(1)PROD := 0
(2)I := 1
(3)T1 := 4 * I
(4)T2 := a0 – 4
(5)T3 := T2[T1]
(6)T4 := 4 * I
(7)T5 := b0 – 4
(8)T6 := T5[T4]
(9)T7 := T3 * T6
(10)PROD := PROD + T7
(11)I := I + 1
(12)if  I ≤ 20 goto (3)

优化后：

(1)PROD := 0
(2)T1 = 0;
(3)T2 := a0 – 4
(4)T5 := b0 – 4
(5)T1 := T1 + 4;
(6)T3 := T2[T1]
(7)T6 := T5[T1]
(8)T7 := T3 * T6
(9)PROD := PROD + T7
(10)if T1 ≤ 80 goto (5)

目标代码生成

目标代码生成的主要问题：

选择合适的指令生成最短的代码
充分利用有限的寄存器

如何充分利用寄存器（自学）

编译原理 课程笔记

第一章 绪论

引言

语言

机器语言、汇编语言、高级语言

翻译

解释

强制式语言、函数式语言、逻辑式语言、对象式语言

绑定

静态和动态

变量的四个属性

第二章 数据类型

第三章 控制结构

第四章 程序语言的设计

前言

文法

文法的形式定义

产生式的简化

文法的表示

文法的分类

推导的表示

句型、句子、语言

文法等价

推导树

第五章 编译

复习概念

编译步骤

词法分析

语法分析

语义分析与中间代码生成

优化

目标代码生成

完整的程序处理过程

编译前端和后端

第六章 词法分析

概述

单词的种类

单词的输出形式

单词类别的划分

状态转换图

词法分析器的转换图

词法分析器

第七章 自上而下的语法分析

引言

回溯分析法

公共左因子

左递归

回溯分析法特点

主要缺陷

递归下降分析法

方法步骤

递归下降分析器的构造

预测分析法

构造 First 集

构造 Follow 集

第八章 自下而上语法分析

概念

算符优先分析法

构造 FIRSTVT 集

构造 LASTVT 集

算符优先关系表

LR 分析法

第九章 语义分析

符号表

语义分析概论

语义分析的主要工作

语法制导翻译

语义值

中间代码

简单赋值语法分析的翻译

语义变量及过程

翻译方案

类型转换

说明语句的翻译

文法

语义变量和过程

翻译方案

控制语句的翻译

布尔表达式的翻译

文法

编译原理课程笔记

第一章绪论

第二章数据类型

第三章控制结构

第四章程序语言的设计

第五章编译

第六章词法分析

第七章自上而下的语法分析

第八章自下而上语法分析

第九章语义分析

第十章代码优化和目标代码生成

第十一章运行时存储空间的组织