参考博客：http://www.cppblog.com/menjitianya/archive/2015/11/02/212171.html

建立树状数组的目的

树状数组 (Binary Indexed Tree) 代码简洁、常数小于线段树，但功能少。即使如此也很常用。（线段树板子长抄着慢）

树状数组的作用是可以log(n)维护在线前缀和（最大最小值什么的也可以？）

树状数组要解决两个东西：

  1. int add(int i, int x) //对一个数进行更新，要求时间复杂度为 O(log n)
  2. int sum(int i) //求[x1,xi]的区间元素和，时间复杂度为 O(log n)

定义

树状数组的定义是一个一维数组 tree[]，其中 tree[i] 表示 [i-(i&(-i))+1,i] 这个区间内 a 数组元素的和。

但这个定义挺迷的，i-(i&(-i))+1 代表什么呢？别急，慢慢往下看，

树状数组虽然是用数组实现的，但他实际上是一棵树形的，如下图。

树状数组
树状数组

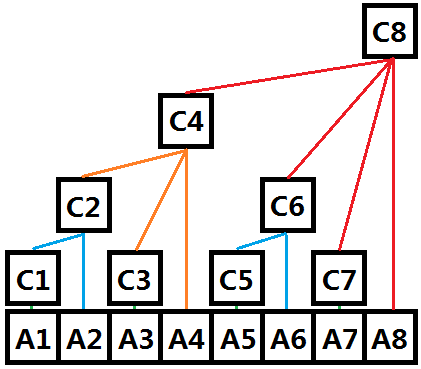
可以看出这棵树中，对于两个数组下标 $x$, $y$, 如果满足 $x+2^k=y$ （$k$ 为 $x$ 的二进制表示中末尾 $0$ 的个数，在后文定义 $lowbit(x)=2^k$），则定义 $y$ 是 $x$ 的父亲。
如 $4$ 的 $k$ 为 $2$，则 $4$ 的父亲即是 $4+2^{k_4}=4+2^2=8$。

$C_i$是什么

每一个结点 $C_i$ 存了它自己和它的所有（递归）子结点的 $A_i$ 值之和。

那么能否用数学表达 $C_i$ 存的是哪些数呢？我们来看看 $C_8$。

\begin{equation}
\begin{split}
C_8 &= C_4 + C_6 + C_7 + A_8\\
&= C_2 + A_3 + A_4 + A_5 + A_6 + A_7 + A_8\\
&= A_1 + A_2 + A_3 + A_4 + A_5 + A_6 + A_7 + A_8
\end{split}
\end{equation}

比较显然的是，$C_i$ 存的是 ${A_i}$ 数列中的连续和，而连续和的右边界一定是 $i$。那么左边界是什么呢？

从图上可以看出，左边界是顺着 $C_i$ 的最左儿子一直找直到找到叶子结点。

那能否用数学来直接推导出左边界呢？

根据父子结点关系可以逆推得到 $C_8$、$C_6$、$C_7$ 的左边界，过程是这样的（为方便观察规律，标注了每个数字的二进制）：

父结点 81000 6110 7111
子结点1 40100 5101
子结点2 20010
子结点3 10001
左边界 10001 5101 7111

结论已经呼之欲出了：对于每个数 $i$，它的左边界是：把 $i$ 最右边的 $1$ 变成 $0$ ，再在这一位的加上 $1$。

顺便提一句，要遍历某个点的子结点，可以取出最右一位的 $1$ 以后，依次往后面的位加 $1$，得到的所有数就是它的所有子结点。
如 $8$ 1000 的子结点就有 $4$ 0100、$6$ 0110、$7$0111。
也可以换一种理解方式，$i$ 的子结点为 $ i-2^k , k \in [0,log_2(lowbit(i))-1]$。

按照上面定义的

$k$ 为 $x$ 的二进制表示中末尾 0 的个数

再定义 $lowbit(x) = 2^{k_x}$，即 $lowbit(x)$ 为 $x$ 最右的一个 $1$，
那么左边界就应该是 $i-lowbit(i)+1$，所以，

$$ C_i = \sum_{j=i-lowbit(i)+1}^{i}{A_i} $$

求和函数 sum(int i)

明白了 $C_i$ 的含义以后，我们可以用它来求 $sum(i)$ 了。用 $lowbit(i)$ 表示 $2^{k_i}$ ，则有

\begin{equation}
\begin{split}
sum(i) &= A[1] + A[2] + … + A[i]\\
&= A[1] + A[2] + … + A[i-lowbit(i)] + A[i-lowbit(i)+1] + … + A[i]\\
&= sum(i-lowbit(i)) + C[i]
\end{split}
\end{equation}

上式可以用递归求解，边界是 $sum[0] = 0$。

用递归形式写就是：

1
2
3
4
int sum(int i)
{
    return i ? C[i] + sum[lowbit(i)] ： 0;
}

可以改写为非递归形式：

1
2
3
4
5
6
7
8
9
10
int sum(int i)
{
    int ans = 0;
    while(i)
    {
        ans += C[i];
        i -= lowbit(i);
    }
    return ans;
}

时间复杂度是 $O(log n)$。

更新函数 add(int i, int x)

更新操作即是把第 $i$ 个数增加 $x$。朴素前缀和要更新 $i$ 及以后的所有前缀和，所以复杂度是 $O(n)$。
可以观察到，树状数组中，所有数的信息只存在该下标对应的结点和它的（递归）父结点的 $C_i$ 中。因此，只需要递归对父结点做同样的加减即可。
根据定义，$i$ 结点的父结点是 $i+lowbit(i)$，代码也就不难写了。
这一过程同样有递归和非递归形式。

递归形式：

1
2
3
4
5
6
7
8
int add(int i, int x)
{
    if(i <= n)
    {
        c[i] += x;
        add(i + lowbit(i), x);
    }
}

非递归形式：

1
2
3
4
5
6
7
8
int add(int i, int x)
{
    while(i <= n)
    {
        c[i] += x;
        i += lowbit(i);
    }
}

$O(1)$ 求 lowbit(x)

可以看到，不管是 add(i,x) 还是 sum(i)，其精髓在于 lowbit(i)，因为

结点 $i$ 的父结点是 $i+lowbit(i)$
结点 $i$ 的子结点为 $ i-2^k, k \in [0,log_2(lowbit(i))-1]$
结点 $i$ 的左边界是 $i-lowbit(i)+1$

上面这两句，很漂亮的诠释了树状数组何为树状。理解了这句话，就可以自己手写树状数组了。

所以呢，最后一步，也是最关键的一步，就是求 lowbit(i) 了。朴素方法（把 $i$ 反复除以2）能在 $O(log\space i)$ 求 $k_i$，但是用位运算的方法可以把这个过程变成 $O(1)$。

由补码的知识可以得到如果不知道的去看原博

lowbit(x) = x & (-x)

补码这种东西虽然不直观，初学者很难懂，但是挺神奇的，比如这里的 x&(-x)，还有原博的例子

(+5) + (-5) = 00000101 + 11111011 = 1 00000000 (溢出了！！！) = 0

至此，再看文章开头对树状数组的定义：

树状数组的定义是一个一维数组 tree[]，其中 tree[i] 表示 [i-(i&(-i))+1,i] 这个区间内 a 数组元素的和。

其实就很好理解了。

实现上，由于 & 的优先级低于 -，可以这么写：

1
int lowbit(int x){return x & -x;}

时间复杂度是 $O(1)$。

至此，树状数组的一般应用就讲完了。初始化的时候，不需要像线段树一样必须要开 $2^n$ 个内存，有多少数开多少内存就够了。把上面提到的三个函数组合起来就能去做最简单的 Point Update Interval Query（点更新，段询问）了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
ll C[maxn] = { 0 };
ll n;
ll lowbit(ll x)
{
    return x & -x;
}
void add(ll i, ll x)
{
    while (i <= n)
    {
        C[i] += x;
        i += lowbit(i);
    }
}
ll sum(ll i)
{
    ll ans = 0;
    while (i > 0)
    {
        ans += C[i];
        i -= lowbit(i);
    }
    return ans;
}

应用：更新区间、查询单元素

树状数组最基础的模型是 Point Update Interval Query（点更新，段询问），但是做一下差分也可以实现 Interval Update Point Query（段更新，点求值）。具体实现略。

应用：求最大值

理论上来说，树状数组也可以 Point Update Interval Query 求区间最大值。

在这篇博客中实现了树状数组求最大值，初始化的复杂度为 $O(nlogn)$，单点维护和区间查询的复杂度都是 $O(log^2n)$。

原理其实就是发生更改以后，遍历、更改所有（递归）父结点；查询的时候，就遍历该区间对应所有结点的值的最大值。

利用好这一句话：

结点 $i$ 的子结点为 $ i-2^k, k \in [0,log_2(lowbit(i))-1]$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
const int maxn = 3e5;
int a[maxn], h[maxn];
int n, m;

int lowbit(int x)
{
    return x & (-x);
}
void update(int x) //x指下标。在求最大值中，原数列必须保留。
{
    int lx, i;
    while (x <= n)
    {
        lx = lowbit(x);
        if (a[x] < h[x])
        	for (i=1; i<lx; i<<=1)
            	h[x] = max(h[x], h[x-i]);
        h[x] = a[x];
        x += lowbit(x);
    }
}
int query(int x, int y)//求[x,y]区间内最大值
{
    int ans = 0;
    while (y >= x)
    {
        ans = max(a[y], ans);
        y--;
        for (; y-lowbit(y) >= x; y -= lowbit(y))
            ans = max(h[y], ans);
    }
    return ans;
}
int main()
{
    //完成对 a[i] 输入以后开始更新 h[i]
    memset(h,0,sizeof(h));
    for (int i = 1; i <= n; i++)
    {
        cin >> a[i];
        update(i);
    }

    //查询 [x, y] 最大值
    ans = query(x, y);

    //更新 a[x] 以后更新单点
    a[x] = y;
    update(x);
}