数模自学笔记——插值和拟合

插值和拟合的概念和区别

插值曲线要过数据点，拟合曲线整体效果更好。

插值需要对准了才能插，拟合要求的是最接近的结果、最好的总体效果。

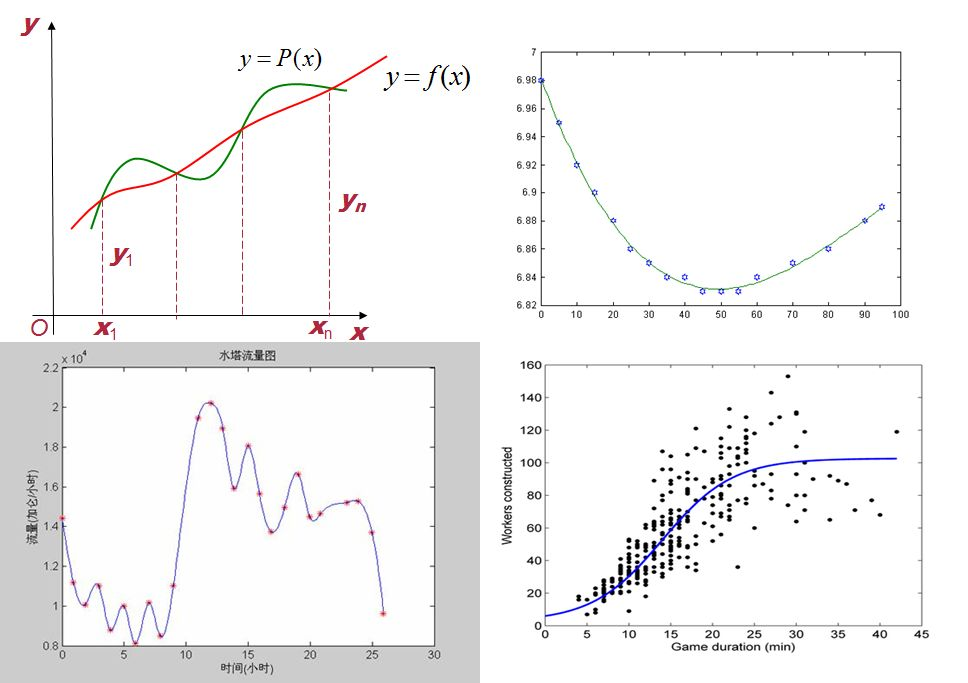
一维插值

变量之中存在的函数关系，有时不能确定，而是通过获得的数据来找出两个变量间可能存在的连续。
——《数学建模算法与应用（第2版）》（司守奎主编）

未知 $f(x)$，但已知 $f(x)$ 的很多观测点 $(x_i, y_i)$，要找一个（可以分段的）函数 $\varphi(x) \approx f(x)$，并且强制要求 $\varphi(x)$ 经过所有观测点。

公式就略写了，要是用到了，看书就行。

分段线性插值

简单的说，就是把每两个节点用直线连接起来。因此其函数表达式也较为显然。

有意思的是，虽然函数计算每点的插值时只用到左右两个点，但这个函数随着点数 $n$ 的增加，收敛于 $f(x)$，即 $\lim\limits_{n\to\infty} I_n(x) = f(x)$。因此也是用的最多的（如利用三角函数表计算任意三角函数值）。

拉格朗日插值

从思想上来说，Lagrange 插值法是通过函数 $f(x)$ 的已知的 $n+1$ 个点 $(x_j, y_j)$，构造出一个多项式 $p(x)$ 来近似 $f(x)$。（这个多项式最高为 $n$ 次，经过全部 $n+1$ 个点）

在 Lagrange 插值中，已知 $n+1$ 个点 $(x_j, y_j)$，则应用 Lagrange 插值公式得到的 Lagrange 插值多项式 为：

$$p(x) \approx \sum_{j=0}^k y_j l_j(x)$$

其中

$$l_j(x) = \prod_{i=0, i \neq j}^n\frac{x-x_i}{x_j-x_i}=\frac{(x-x_0)}{(x_j-x_0)} \cdots \frac{(x-x_{j-1})}{(x_j-x_{j-1})} \frac{(x-x_{j+1})}{(x_j-x_{j+1})} \cdots \frac{(x-x_{k})}{(x_j-x_{k})}$$

但也是介绍一下概念，并没有太多展开。

样条插值

样条 spline 插值的目标就是使函数连续，且在连接处具有连续的曲率。

即，在每一段上 $S(x)$ 是 m 次多项式，且在整段上，$S(x)$ 具有 $m-1$ 阶导数，则称 $S(x)$ 为样条函数。使用样条函数作为结果，就是样条插值。

由于 $m=1$ 时，不用考虑其导数，因此分段线性插值也是样条插值（23333

三次样条插值

考虑次数为三的样条插值。由上面的定义我们可以设 $n$ 个区间的表达式为：

$$S_i(x) = a_i x^3 + b_i x^2 + c_i x + d_i$$

共有 $4n$ 个待定系数。

条件对应的方程有：

(1) $S(x)_i=y_i (i=1,2,..n)$；
(2) 相邻两段的函数值、一阶导数、二阶导数在临界点相同。

共 $(4n-2)$ 个表达式，还需给出两个表达式。由此引出了三个版本的样条插值。

$S’(a)=y_0’, S’(b)=y_n’$。这叫完备三次样条插值函数。
- 若令 $y_0’ = y_n’ = 0$，样条曲线在端点呈水平状态。
- 若以 $x_0 \sim x_3$ 求三次 Newton 插值多项式（不懂这是什么）$N_a(x)$，以 $x_{n-3} \sim x_n$ 求三次 Newton 插值多项式$N_b(x)$，然后令 $S’(a)=N’_a(a), S’(b)=N’_b(b)$，这叫 Lagrange 三次样条插值函数。
$S’’(a)=y_0’’, S’’(b)=y_n’’$。这叫自然边界条件。
$S’’(a)=S’’(b), S’(a)=S’(b)$，这叫周期条件。

MATLAB 插值工具箱

一维插值

1	y = interp1(x0, y0, x, <method>)

其中 <method> 可选：

'nearest'：最近项插值
'linear'：线性插值（默认）
'spline'：立方样条插值，边界条件为 'not-a-knot'（见下）
'cubic'：立方插值

立方样条插值

立方样条插值更推荐使用 csape：

1 2	pp = scape(x0, y0, <conds>, <valconds>); % pp 是 polynomial pieces，多项式分段（函数） y = fnval(pp, x);

其中 <conds> 为：

留空，使用 Lagrange 边界条件
'complete'：完备立方样条插值，即边界为一阶导数值，值在 <valconds> 中给出，若留空则按 Lagrange 边界条件
'not-a-knot'：非扭结条件，即要求前两段表达式的三阶导数相等，且后两段的三阶导数相等，在没有边界条件时常用
'periodic'：周期条件，即 $S’’(a)=S’’(b), S’(a)=S’(b)$
'sencond'：边界为二阶导数值，值在 <valconds> 中给出，若留空则取 $[0,0]$

顺便，还可以将 fnval 改写为匿名函数，然后跑积分：

x0 = [0 3 5 7 9 11 12 13 14 15];
y0 = [0 1.2 1.7 2.0 2.1 2.0 1.8 1.2 1.0 1.6];
x = 0:0.02:15;

pp = csape(x,y);
int1 = integral(@(t)fnval(pp,t), 0,15)  % int1 = 22.5788

这和 interp1 后运用积分定义 $\int_a^b f(x)dx = \lim_{n\to\infty}\sum_{i=1}^n f(x_i)$（其中 $x_i$ 取两端点的平均值）求得的结果非常接近。

x0 = [0 3 5 7 9 11 12 13 14 15];
y0 = [0 1.2 1.7 2.0 2.1 2.0 1.8 1.2 1.0 1.6];
x = 0:0.002:15;
method = "spline";
y = interp1(x0, y0, x, method);

int2 = (sum(y)-(y(1) + y(end))/2) * 0.002 % int2 = 22.5788

二维插值

二维插值，即节点为二维的插值问题。如测定了若干点的海拔（结点值），然后更精确的绘图。

这里不讲原理，直接讲应用了。

1	z = interp2(X0, Y0, Z0, X, Y, <method>)

其中 X0 Y0 Z0 为大小相同的网格变量。如果读者不清楚什么是网格变量，或数据不是以网格变量给出的、而是以 x y 向量形式给出的，请参考 meshgrid。

<method> 与一维插值相同。

同时，二维的三次样条插值仍然可以使用 csape，只是输入参数有所变化。如需要，请自行查阅 MATLAB 文档。

如果输入的是散乱的 $n$ 个节点的 $x$、$y$、$f(x,y)$ 值，可以使用 griddata 进行插值：

1	Z = griddata(x0, y0, z0, X, Y, <method>)

<method> 与一维插值相同。

曲线拟合与最小二乘法

曲线拟合就是给定 $n$ 个点，寻求一个函数 $f(x)$ 与给定的点在某种准则下最为接近，即拟合的最好。

线性最小二乘法是最常用的方法，其基本思想为，设

$$f(x) = a_1r_1(x) + a_2r_2(x) + \cdots + a_nr_n(x)$$

其中 $r_k(x)$ 为事先选定的一组线性无关的函数；$a_k$ 为待定系数。

拟合目标（准则）是使得 $y_i$ 与 $f(x_i)$ 的距离 $\delta_i$ 的平方和最小，称为最小二乘准则，即

$$\min_{a_1, a_2, \cdots a_n} J=\sum_{i=1}^n \delta_i = \sum_{i=1}^n [f(x_i)-y_i]^2$$

可由线性代数知识证明，$r_k(x)$ 一旦确定且线性无关，则 $\{a_1, a_2, \cdots a_n\}$ 有唯一的解。

现在的问题就在于 $r_k(x)$ 的选取。如果通过机理分析（通过对数据和现象的分析对事物内在规律做出的猜想、模型假设）能知道 $x$ 和 $y$ 的函数关系，就很容易了。如果不知道，则一般可以通过作图，然后直观地判断应该用什么样的函数。常见的曲线有：

直线 $y=a_1x+a_2$
多项式 $y=a_1x^m + \cdots + a_mx + a_{m+1}$（一般 $m=2,3$，不宜太高）
单支双曲线 $y = \frac{a_1}{x} + a_2$
指数函数 $y = a_1e^{a_2x}$

最小二乘法 MATLAB 代码

由于上述的证明 $\{a_1, a_2, \cdots a_n\}$ 有唯一的解过程略，这里不写运用原理解最小二乘法。如需要，可查阅《数学建模算法及应用（第二版）》。

多项式拟合可使用 polyfit。也可以直接使用带 GUI 的工具箱函数 cftool。

1 2	a = polyfit(x0, y0, m); % m 为次数，a 为多项式拟合的系数组成的向量 y = polyval(a, x); % 多项式求值

最小二乘规划

上面求参数 $\{a_1, a_2, \cdots a_n\}$ 的过程，可以说是是在求参数值使得目标函数值最小。咦，这不就是最优化问题吗？

所以这里的内容其实回到了规划问题，只是目标函数变成了最小二乘（least square，lsq）的形式，即目标函数变为

$$\min F(\boldsymbol{x}) = \sum_{i=1}^m f_i^2(\boldsymbol{x}),\quad\boldsymbol{x}\in \mathbf{R}^n$$

注意这里的向量 $\boldsymbol{x}$ （下同）实际上是参数，对应上面的 $f(x)$ 中的参数 $\{a_1, a_2, \cdots a_n\}$；
而这里的 $f_i(\boldsymbol{x})$ 对应的是上面的 $\delta_i = [f(x_i)-y_i]$。

对于这类规划问题，MATLAB 提供了以下函数，现整合为下表，且一并包含了 polyfit 函数：

函数名	适用情况	输入参数中的 $(x_i, y_i)$ 数据处理
`polyfit`	对参数为线性函数对 $\boldsymbol{x}$ 为多项式函数	无需处理，直接作为函数参数
`lsqlin`	对参数为线性函数	需转化为对应矩阵元素
`lsqcurvefit`	对参数可为非线性函数	无需处理，直接作为函数参数
`lsnonlin`	对参数可为非线性函数	需转化为对应关于参数的函数
`lsqnonneg`	对参数为线性函数要求参数非负	需转化为对应矩阵元素

上表中的“对参数为线性函数”指 $f_i(\boldsymbol{x})$ 对于 $\{a_1, a_2, \cdots a_n\}$ 为线性函数。一个非线性的例子是：$y=e^{-a_1x_1}\sin(a_2x_2)$。

顺便一提，由于最小二乘问题能化为二次规划问题，lsqlin 能解决的问题也可以使用 quadprog 解决。

最后，说了这么多，可能还是 cftool 好用（逃

曲线拟合与函数逼近

上面的是用曲线去接近一些离散点的数据，下面考虑用一个（简单的）曲线接近一个（复杂的）函数曲线，这便是函数逼近。

与曲线拟合的最小二乘准则对应，函数逼近常用最小平方逼近，即

$$\min_{f(x)} J = \int_a^b [f(x)-y(x)]^2$$

就是把 $y_i$ 改成 $y(x)$，把求和改成积分。合理。

之后的理论证明和解释因为有点高深，故略过，直接放一个例题的代码，以后需要的时候就照搬叭。

求 $f(x)=\cos x, x \in [-\frac{\pi}{2}, \frac{\pi}{2}]$ 在 $H = {\rm Span}\{1, x^2, x^4\}$ 中的最小平方逼近多项式。

syms x
base=[1,x^2,x^4];
y1=base.'*base
y2=cos(x)*base.'
r1=int(y1,-pi/2,pi/2)
r2=int(y2,-pi/2,pi/2)
a=r1\r2
xishu1=double(a)  % 符号数据转化成数值型数据
xishu2=vpa(a,6)   % 把符号数据转化成小数型的符号数据

解得 xishu1 = 0.9996 -0.4964 0.0372，即所求最小平方逼近多项式为

$$y = 0.9996 - 0.4964x^2 + 0.0372x^4$$

例题黄河小浪底调水调沙问题

由于这部分内容比较简单，在数模中多是作为题目中的一个小点，因此纯插值拟合的题不难。

题目来源：《数学建模算法与应用（第2版）》（司守奎主编）节 5.5

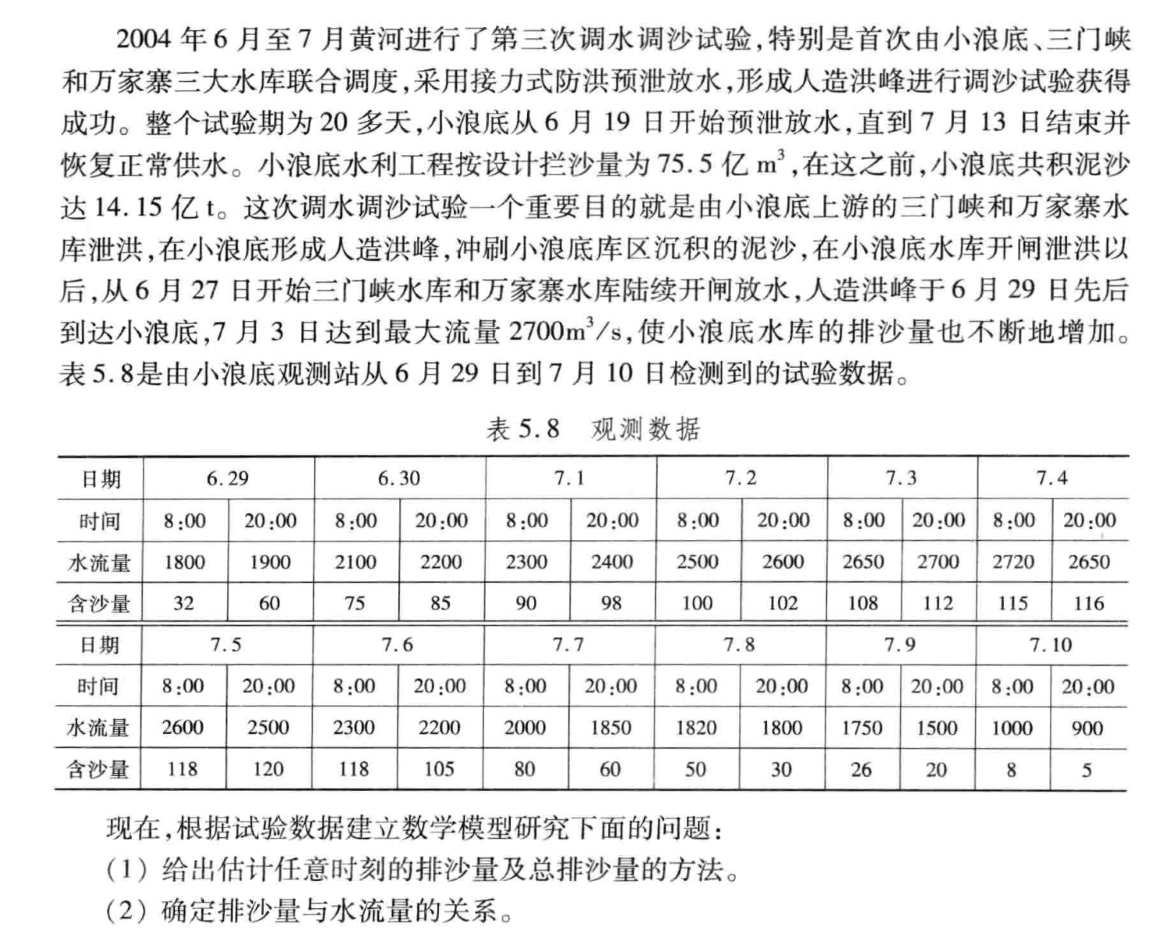
题目重述略。

问题分析

问题一要求我们通过给定 24 个时刻的数据，估计任意时刻的数据以及总排沙量，我们采用插值的方式得到任意时刻的数据，再对插值函数进行积分得到总排沙量。

问题二要求我们确定排沙量与水流量的关系，我们对数据进行拟合即可。

变量及名词解释

符号	含义
$t$	观测时刻，以 6 月 29 日零点开始计时，以秒为单位
$w_t’$	观测到 $t$ 时刻的水流量，单位 $m^3/s$
$s_t’$	观测到 $t$ 时刻的含沙量，单位 $kg/m^3$
$S_t’$	观测到 $t$ 时刻的排沙量，单位 $kg/s$
$S(t)$	估计排沙量关于时刻的函数
$S$	整个过程的总排沙量
$t_k$	第 $k$ 次观测的时间点
$S(w)$	估计排沙量关于水流量的函数

模型建立与求解

问题一

由于题目的时间是以日期、时分给出的，我们需将其化为以秒为单位的正整数。可得以下关系：

$$t_k = 3600(12k-4) \quad k = 1,2,\cdots,24.$$

由物理公式可知，排沙量=含沙量*水流量，即：

$$S_t’ = s_t’ w_t’$$

通过数据处理我们可以得到观测到的每个时刻的排沙量。

对这些数据进行三次样条插值，边界条件为非扭结条件，则可得到任意时刻的估计排沙量 $S(t)$。代入任意时刻即可求得该时刻的估计排沙量。

对 $S(t)$ 进行积分，就能得到总的排沙量。

编写 MATLAB 代码如下：

hold off;
data = [
    1800	1900	2100	2200	2300	2400	2500	2600	2650	2700	2720	2650	2600	2500	2300	2200	2000	1850	1820	1800	1750	1500	1000	900;
    32	60	75	85	90	98	100	102	108	112	115	116	118	120	118	105	80	60	50	30	26	20	8	5
];
t = 3600*(8:12:8+23*12);
sand = data(2,:) .* data(1,:);

T = t(1):t(end);

% 插值
pp = csape(t,sand,"not-a-knot");
Sand = fnval(pp,T);
SandTotal = integral(@(t)fnval(pp,t),T(1),T(end));

% 输出排沙量和时间的函数关系图
fplot(@(t)fnval(pp,t),[t(1) t(end)],'b-');
hold on;
plot(t,sand,'r*');
hold off;
pause

% 输出总排沙量和时间的函数关系图
f = @(time) integral(@(t)fnval(pp,t),T(1),time);
fplot(f,[t(1) t(end)])

得到函数图及输出如下：

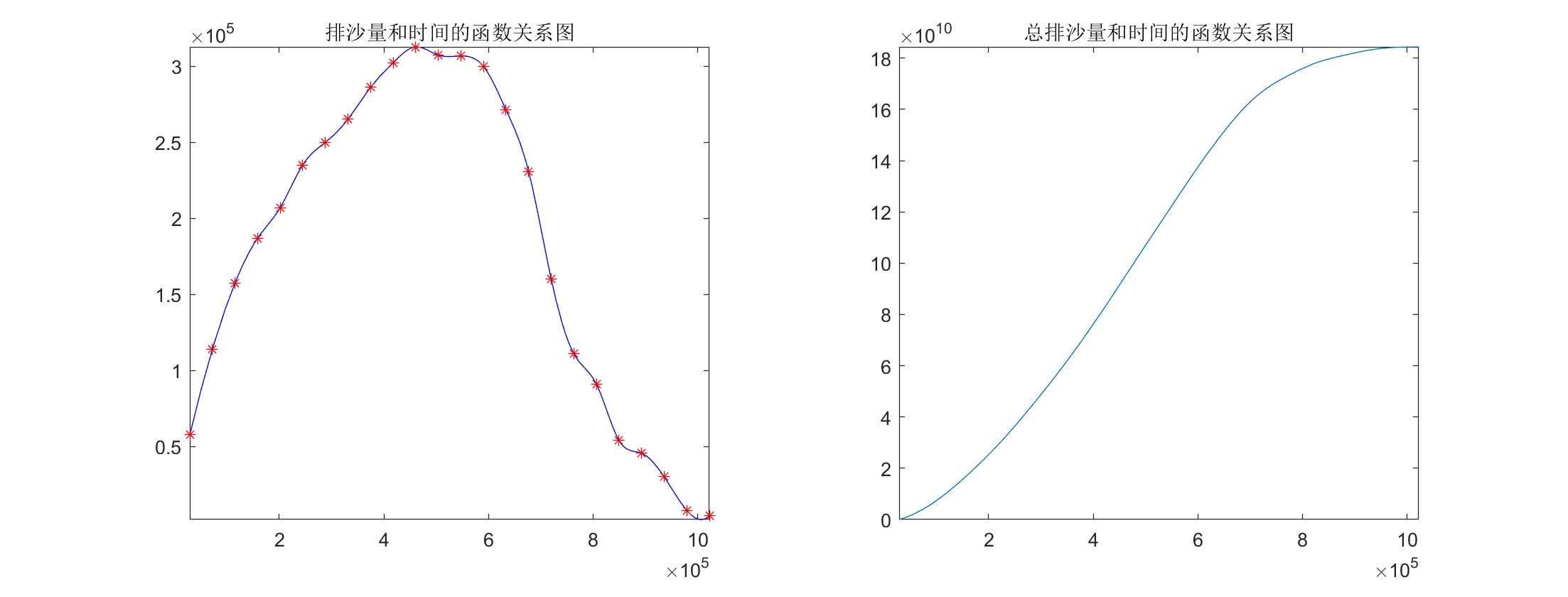
计算得从第一个检测时刻到最后一个检测时刻，共排沙约 $1.8440\times 10^{11} kg$。

问题二

问题二要求我们用已知数据拟合出排沙量 $S_t’$ 和水流量 $w_t’$ 的函数关系。

考虑到 7.4 8:00 时水流量最大，以该时刻为临界的前后两个时段可能是不同的状态，我们对函数分段进行拟合，前一段为 6.29 8:00 至 7.4 8:00，后一段为 7.4 8:00 至 7.10 20:00。其中中间时刻 7.4 8:00 被计算两次。

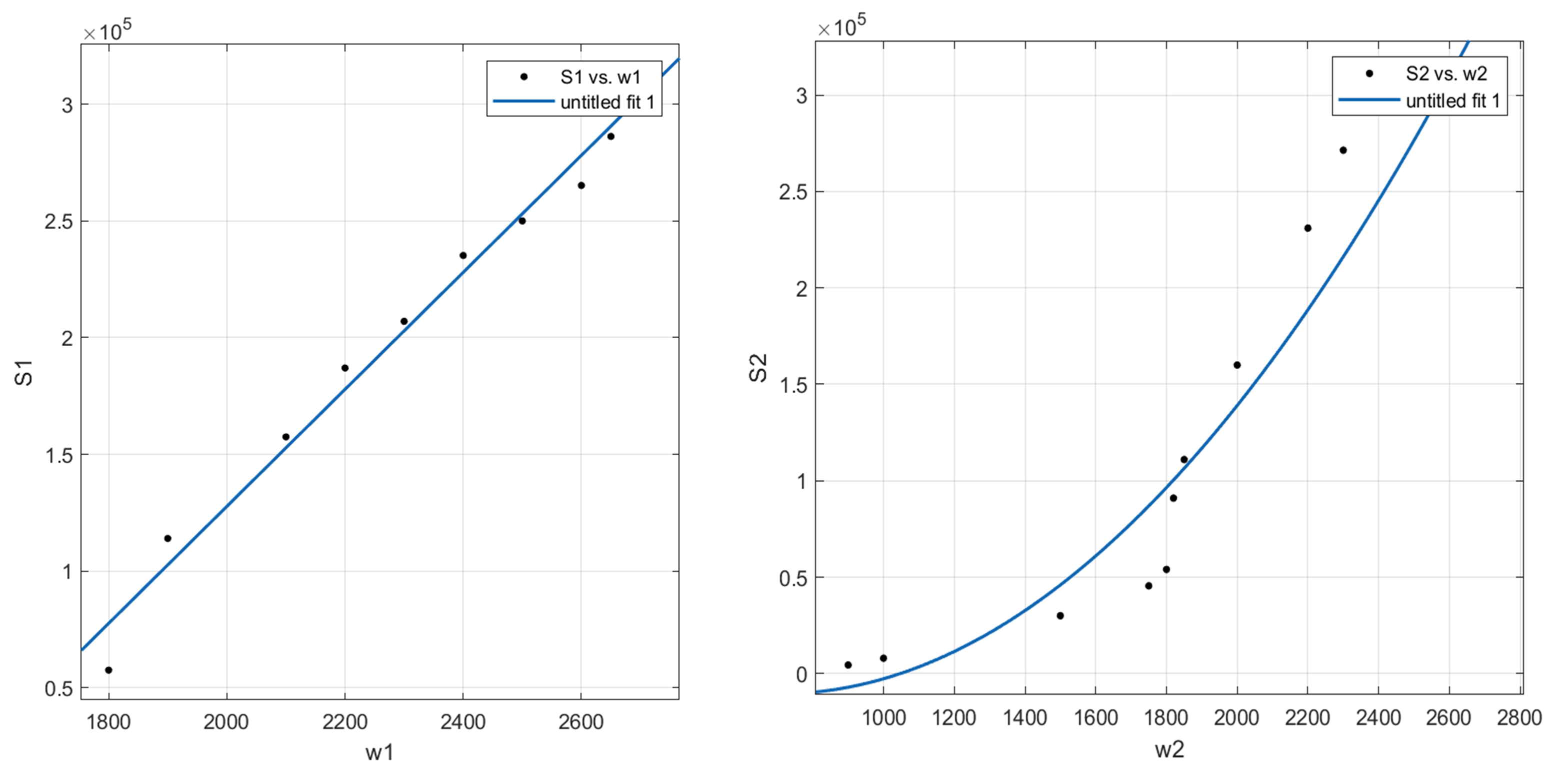
由于我们并不清楚其函数关系，所以先以上述数据绘制两幅散点图，然后使用 cftool 进行拟合。

编写 MATLAB 代码如下：

data = [
    1800	1900	2100	2200	2300	2400	2500	2600	2650	2700	2720	2650	2600	2500	2300	2200	2000	1850	1820	1800	1750	1500	1000	900;
    32	60	75	85	90	98	100	102	108	112	115	116	118	120	118	105	80	60	50	30	26	20	8	5
];
t = 3600*(8:12:8+23*12);
sand = data(2,:) .* data(1,:);

T = t(1):t(end);

w1 = data(1,1:11);
w2 = data(1,11:24);
S1 = sand(1:11);
S2 = sand(11:24);

nexttile;
plot(w1,S1, '*');
title('前半段的散点图');
nexttile;
plot(w2,S2,'*');
title('后半段的散点图');
cftool

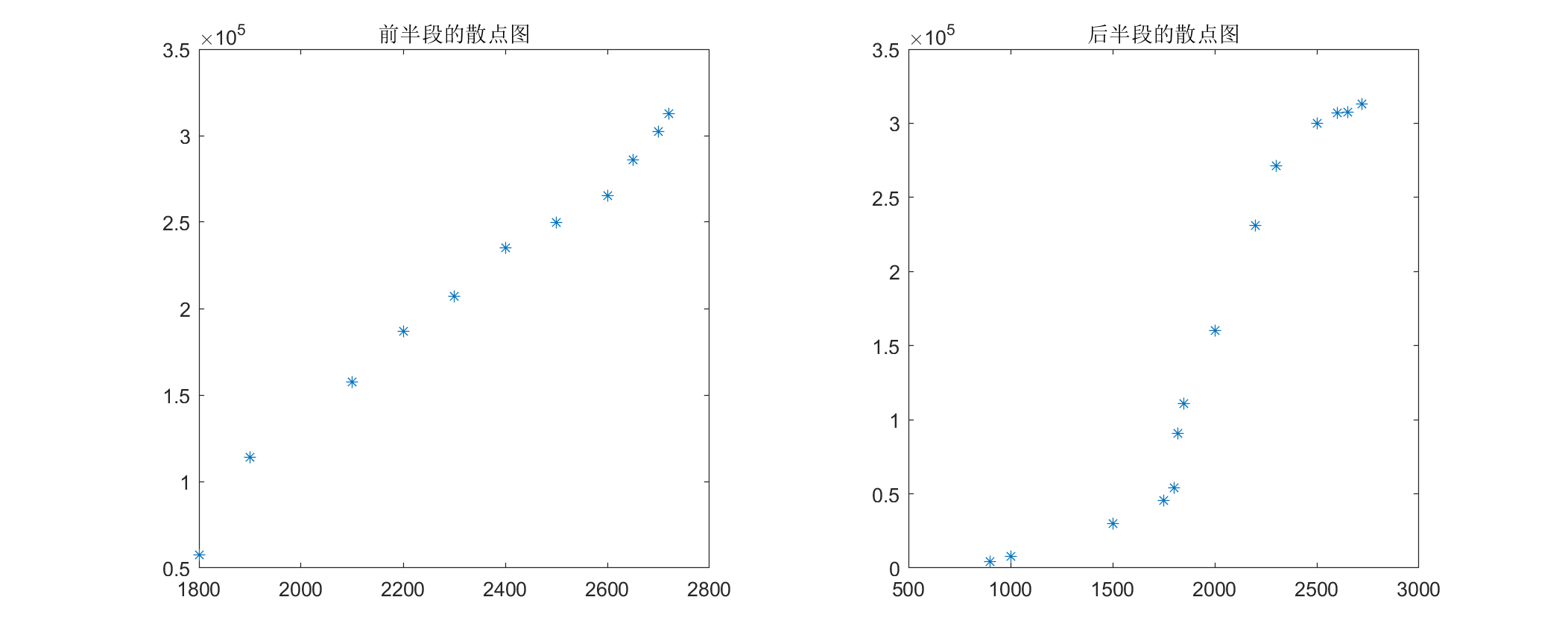
我们考虑对左图使用线性函数拟合，右图使用二次曲线拟合，并验证其 $R^2$ 值。

对于左图，使用线性拟合的结果为 $S_1(w) = 250.6w -3.734\times 10^5$，$R^2=0.986$；
对于右图，使用二次曲线拟合的结果为 $S_2(w) = 0.08882w^2 - 124.8w + 3.332\times 10^4$，$R^2=0.9408$（相比一次下 $R^2=0.8837$）。

综上，

$$S(w) = \begin{cases}
250.6w -3.734\times 10^5 & t < t_{11} \\
0.08882w^2 - 124.8w + 3.332\times 10^4 & t \geq t_{11}
\end{cases}$$

数模自学笔记——插值和拟合

插值和拟合的概念和区别

一维插值

分段线性插值

拉格朗日插值

样条插值

三次样条插值

MATLAB 插值工具箱

一维插值

立方样条插值

二维插值

曲线拟合与最小二乘法

最小二乘法 MATLAB 代码

最小二乘规划

曲线拟合与函数逼近

例题 黄河小浪底调水调沙问题

问题分析

变量及名词解释

模型建立与求解

问题一

问题二

例题黄河小浪底调水调沙问题