1 Introduction

什么是并行计算

  • 并行计算 (parallel computing)：在同一个计算机体系的多个处理器/电脑一起工作解决一个问题
  • 分布式计算 (distributed computing)：分布在多个计算机体系（异地）的处理器/电脑一起工作解决一个问题
  • 并行计算机 (parallel computer)：一个多核的计算机系统
    • 并行计算机分为多计算机系统和中心化多处理器
    • 多计算机系统 (multicomputer)：多个计算机通过内部网络连接
    • 中心化多处理器 (centralized/symmetrical multiprocessor, SMP)：一个计算机系统，其中所有 CPU 共享一个全局内存

并行计算多用于科学计算，分布式计算多用于可靠性、可用性、性价比高的计算。

为什么需要并行计算

  • 微处理器性能增长越来越慢
  • 同样的性能下，并行系统功耗更低

并行计算关心的问题

不懂的地方都给出英文原文……

  • 架构上的问题：
    • Pipline, ILP…
    • 缓存一致性
    • 单共享总线 or 网络
    • UMA, NUMA, CC-NUMA, Cluster…
  • 编程模型上的问题：
    • 单寻址空间 or 多寻址空间
    • 进程使用锁、消息传递 or 其他方法进行同步
    • 分布式 or 中心化内存
    • 故障可靠性
  • 性能表现上的问题：
    • 指标：规模、加速比、可扩展性
    • Models: PRAM，BSP，PPRAM…
    • 并行计算的评价方法
  • 其他问题：
    • 编程语言
    • 编程工具
    • 可移植性
    • Automatic programming of parallel computers
    • Education of parallel computing philosophy

如何编写并行程序

  • 需要明确告诉不同处理器如何分工
  • 需要把串行程序改写为并行
  • 有时候直接改写的效率非常低，需要设计全新的算法

举个栗子

例子：求 n 个函数值的和，其串行算法如下：

1
2
3
4
5
6
sum = 0;
for (i = 0; i < n; i++)
{
    x = compute_next_value(...);
    sum += x;
}

假设我们有 p 个核 (p < n)，每个核计算一部分：

1
2
3
4
5
6
7
8
my_sum = 0;
my_first_i = ...;
my_last_i = ...;
for (my_i = my_first_i; my_i < my_last_i; my_i++)
{
    my_x = compute_next_value(...);
    my_sum += my_x;
}

计算后的结果存在私有变量 my_sum 中。

所有核计算完成后，他们将结果发送至班长（一般就设 0 号核为班长），班长负责计算最终的总和。

1
2
3
4
5
6
7
8
9
if (I am the master core) {
    sum = my_x;
    for each core other than myself {
        receive value from core;
        sum += value;
    }
} else {
    send my_x to the master;
}

更好的并行策略是，不要让班长核做所有的合并工作，而是均摊高每个核上。

对于这个问题，可以两两组合：

Work with odd and even numbered pairs of cores. Pair the cores so that core 0 adds its result with core 1’s result，Core 2 adds its result with core 3’s result, etc.
Repeat the process now with only the evenly ranked cores. Core 0 adds result from core 2. Core 4 adds the result from core 6, etc.
Now cores divisible by 4 repeat the process, and so forth, until core 0 has the final result.

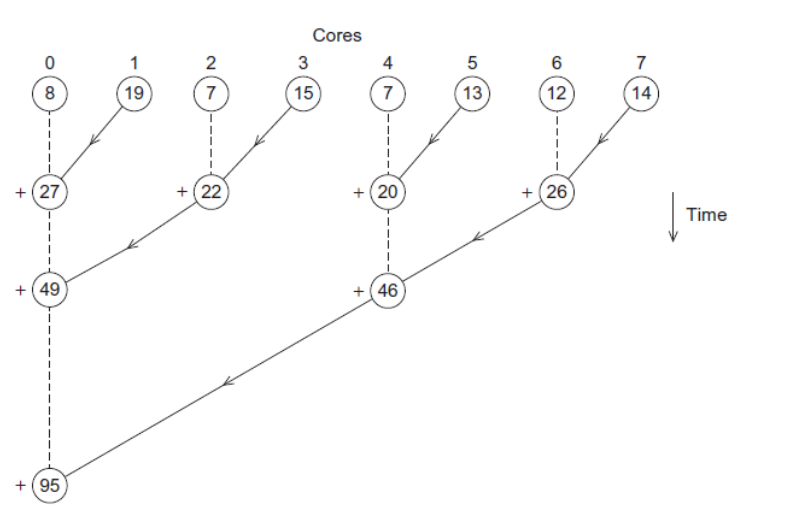
两两组合的求和算法
两两组合的求和算法

这种算法中，班长只进行了 3 次通信 + 3 次求和，相较刚开始的 7 次通信 + 3 次求和。如果核数更多，这样优化的效果会更加显著。

但是，越复杂的问题，并行的难度会更大（比如翻译程序）。所以我们需要编写并行程序来提高多核的利用率。

并行程序的编写方向

  1. 任务并行：将整个任务分成很多不同的小任务
  2. 数据并行：将数据进行分块，每个核在自己分到的数据上做相似的任务

例子：3 个老师（A、B、C）批改 300 张试卷，每张试卷 15 题。

  • 任务并行（将试卷按题目进行划分）：A 老师批改 1-5 题，B 老师批改 6-10 题，C 老师批改 11-15 题
  • 数据并行（将试卷按张数进行划分）：每位老师各批改 100 张试卷

习题

在求和的栗子中，设计一个分配任务的函数（该函数负责计算每个核的 my_first_i 和 my_last_i），使得 $n$ 个任务尽量均匀地分布在 $p$ 个核上。

（这个题目后面应该会讲）

一个优秀的算法是：

$$my\_first\_i = \lfloor\frac{i*n}{p}\rfloor\\
my\_last\_i = \lfloor\frac{(i+1)*n}{p}\rfloor - 1
$$

其中 $i$ 为当前核的下标，从 0 开始。

my_last_i 比较好理解，因为任务分配是连续的，my_last_i 就是 下一个核的 my_first_i 减 1。

至于 my_first_i 的由来我也没想清楚，但是它可以保证所有任务的数量差不超过 1，很均匀。

各位不妨写一个程序模拟一下分配情况，看看每个在不同的 n、p 下，每个核被分了多少个任务、规律是怎么样的。如，在 n=30，p=9 时，该算法会这样分配：

1
3 3 4 3 3 4 3 3 4

2 Parallel Programming Platform

对冯诺依曼体系的改进

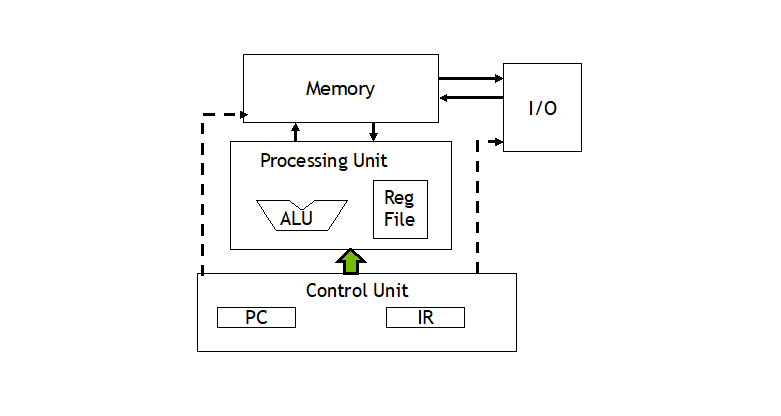
冯诺依曼体系
冯诺依曼体系

冯诺依曼的核心是：存储程序，顺序执行。

该体系的瓶颈一般是 CPU 和内存分离。

改进分为三个方向：

  1. 缓存
  2. 虚拟存储
  3. 底层的并行（指令集并行、线程级并行）

缓存

缓存：比主存更快的存储。一版用户存放物理上接近、且经常使用的数据和指令。

局部性原理略。

缓存分为 3 级。

3 级缓存
3 级缓存

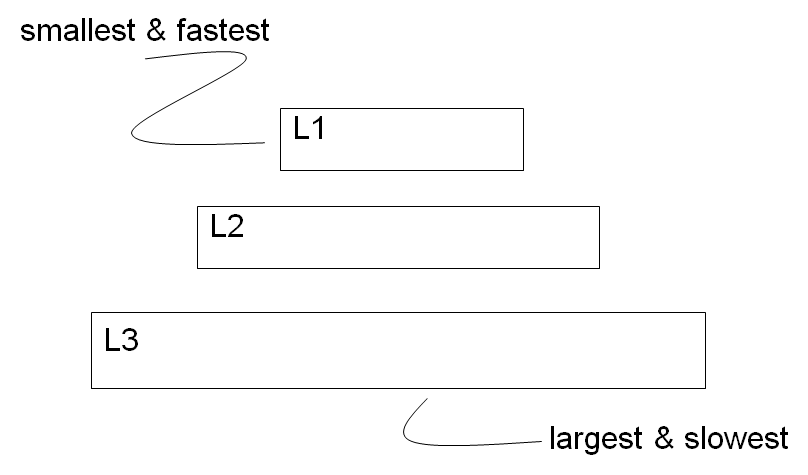
Cache 命中（Cache hit）和不命中（Cache miss）

缓存的写策略

当 CPU 更新缓存的数据时，缓存数据可能会和主存不同。此时有两种策略：

  1. Write-through（写直达）：更新缓存的同时更新主存；缓存和主存始终一致，但每次写缓存的速度会变慢。
  2. Write-back（写回）：更新缓存时标记缓存为脏数据（dirty），当该行缓存被替换时，脏数据会被写回至主存；写缓存的速度不受影响，但缓存替换时的速度会变慢。
缓存的映射方法
  1. 全映射：每行内存可以映射在缓存的任意位置
  2. 直接映射：每行内存只能映射在缓存的固定位置（一般是内存行数下标 % 缓存总行数）
  3. n 路组相联映射：将缓存每 n 行分为一组，每行内存可以映射在缓存的固定的组的 n 行中任意一行（一般组号 = 内存行数下标 % 缓存总行数 % n）

使用全映射或 n 路组相联映射，还需要考虑替换策略，常见的可以使用 LRU。

缓存优化的技巧

缓存对于应用程序和程序员是透明的（不能直接控制缓存），但如果知道局部性原理，可以通过改变程序顺序、间接控制缓存，进而优化速度。

  1. 合并数组（data merge）：通过将两个独立数组合并为一个复合元素的数组来改进空间局部性
  2. 循环交换（loop interchange）：通过改变循环嵌套来按序访问存储器中存储的数据
  3. 循环合并（loop fusion）：将两个具有相同循环类型且有一些变量重叠的独立循环合并
  4. 块化（blocking）：通过不断使用一些数据块（而不是完整地遍历一行和一列）来改进时间局部性
循环优化前后的代码
循环优化前后的代码

假设缓存大小为 4。第一种循环会发生 4 次缓存未命中、第二种循环会发生 16 次缓存未命中。（注：缓存的机制是，每次缓存不命中会将所在行的 4 个元素全部装进缓存）

虚拟内存

虚拟内存的大小大于主存，会将不活跃的程序换到磁盘，活跃的程序放到主存，加快速度。

指令级并行
  1. 流水线技术，参考计算机系统结构
  2. 某些情况下，多条指令也可以被同时发射
  3. 分支预测
线程级并行

略。

并行计算的硬件

  1. SISD（传统冯诺依曼模型）
  2. SIMD：对多个数据进行相同操作，1 个控制单元 + 多个 ALU
  3. MISD（尚未开发）
  4. MIMD：使用多个指令流同时操作多个数据流，多个独立操作单元 + 各自的 ALU

MIMD 物理组织

从上到下越来越离散：

  1. 共享缓存架构（Shared Cache Architecture），多为单芯片多处理器
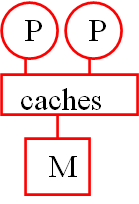
共享缓存架构
共享缓存架构
  1. 统一内存寻址（Uniform Memory Access，UMA）
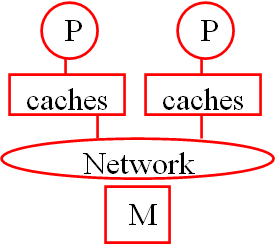
统一内存寻址（UMA）
统一内存寻址（UMA）
  1. 独立内存寻址（Non-Uniform Memory Access，NUMA）

NUMA 并不是处理器完全不能访问其他块的内存，而是处理器可以直接访问一部分内存+通过处理器内置的特殊硬件访问其他内存。

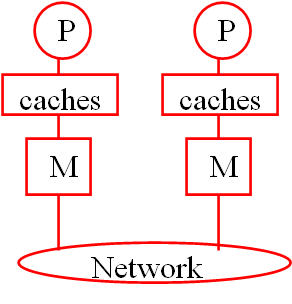
独立内存寻址（NUMA）
独立内存寻址（NUMA）
  1. 分布式系统/内存、集群（Distributed System/Memory）
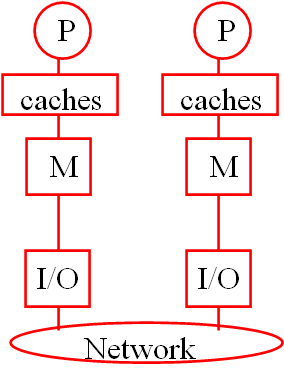
分布式系统/内存
分布式系统/内存

共享内存系统

略。

互连网络

网络的类型、网络的性能指标的一堆概念略。

多维 Mesh 网络

Mesh：将一维线性的网络拓展到二维、三维或更高维度，结点之间只能和邻居进行交流。

超立方体结构

超立方体结构：$d$ 维的超立方体有 $p=2^d$ 个结点。

对超立方体进行编号，可以按照如图的规律：

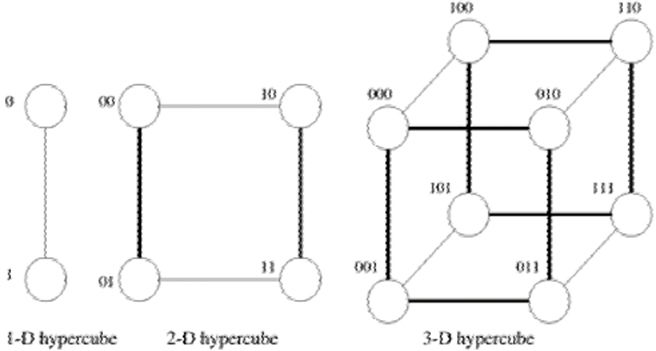
三维及以下的超立方体
三维及以下的超立方体

每个 $d$ 维的超立方体可以分成两个相同的 $d-1$ 维超立方体，编号分别以 0 和 1 开头，且两个子超立方体对应结点的编号除第一位外相同。

按此法可以构造出四维超立方体。

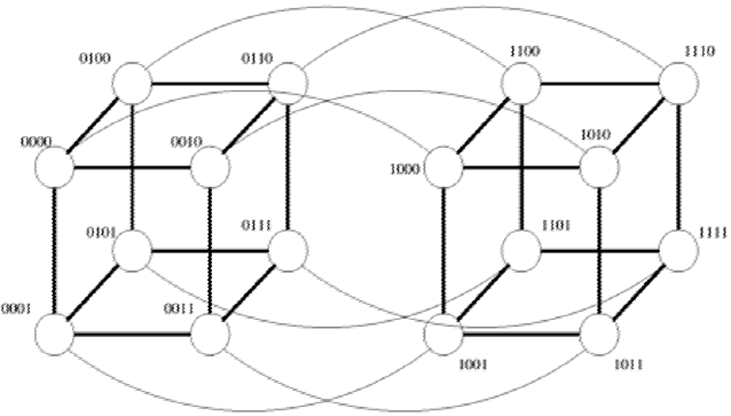
四维超立方体
四维超立方体

该编号方案还有一个性质：两个结点的距离等于这两个结点的汉明距离（不同的位的数量）。如在图中，0110 和 0101 的距离为 2。该性质在使用超立方体构造并行算法时会很有用。

缓存一致性

缓存的写策略有 Write-back 和 Write-through。在 UMA 架构下，多个处理器有各自的缓存，共用内存。

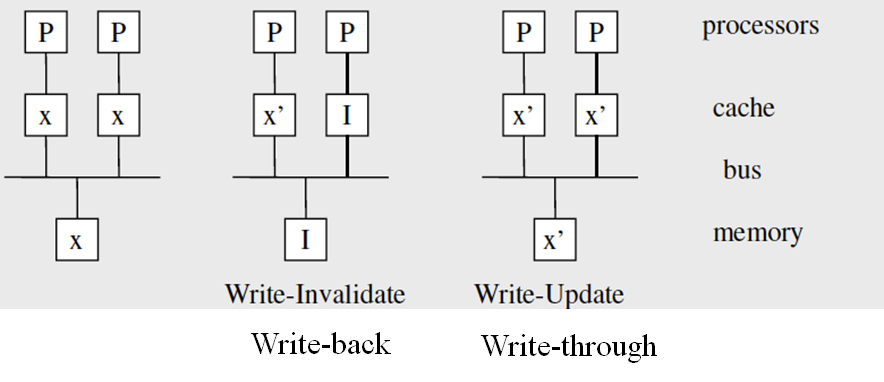
UMA 架构下的缓存一致性协议
UMA 架构下的缓存一致性协议

于是，出现了两个新的概念：

  • Write Invalidate：处理器写自己的缓存时，使其他缓存失效；Write-through 下还需要更新内存，Write-back 下需要使内存失效。
  • Write Update：处理器写自己的缓存时，立即更新其他缓存；Write-through 下还需要更新内存，Write-back 下需要标记缓存为脏，在缓存失效的时候写回内存。

两种策略在什么情况下性能更好？（猜测是在不同核频繁更新不同数据时，写失效更好；多个核都在频繁写同一个数据时，写更新更好。）

现代计算机都默认使用写失效策略。（猜测是因为局部性原理，多核读不同数据的情况更多）

写失效协议

三种状态：Shared、Invalid、Modified（MSI）

  • Shared：存在多份有效的数据（写会导致其他失效）
  • Modified：只有当前数据有效（写不会导致其他失效）
  • Invalidate：数据无效（读会请求数据）
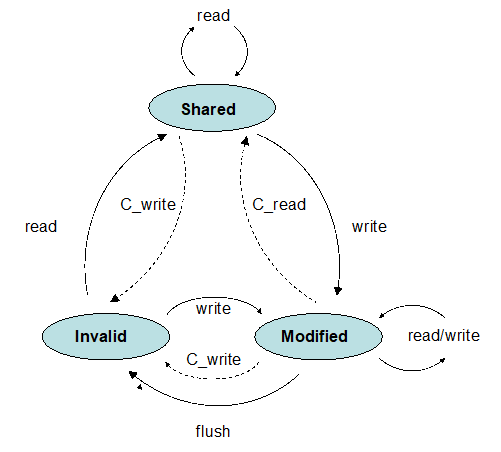
三状态转换图
三状态转换图

硬件条件：所有核共享一个总线，可以用于广播。当 0 号处理器更新了 x，会广波这个消息，其他核听到（snoop）以后就会把自己的 x 标记为 Invalid。

  1. 当一个数据是 Modified 后，所有操作都直接在本地进行，无需向外部广播。
  2. 多个核读入一个数据时，所有缓存的内容都会变为 Shared，随后所有的读操作都直接在本地进行，无需向外部广播。
  3. 多个核同时读和写时，会出现（在带宽上的）瓶颈
基于目录的缓存一致性协议
  • 基于目录：共享的状态都存储在（位于内存的）“目录”
  • 目录里用一位表示 shared/dirty 状态（State）
  • 目录里用一个 bitmap 表示数据被缓存在哪些处理器（Presence Bits）
目录
目录
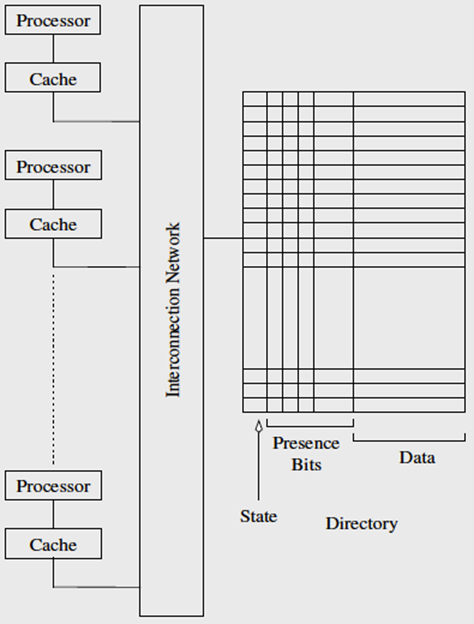
  1. 处理器 0 和处理器 1 读 x，此时状态为 shared，0 和 1 的 presence bits 均为 1
  2. 处理器 0 写变量，状态变为 dirty，1 的 presence bits 为 0
  3. 处理器 2 读变量，将会请求处理器 0 写回，随后 0 和 2 的 presence bits 均为 1

该方案的开销主要是通信开销、以及可能出现频繁的争端。

如果一个并行程序需要大量的一致性操作（大量的读/写共享数据块），目录最终会限制它的并行性能。

还可以分布式的目录系统，但是这里就学了。

False Sharing

不懂

并行计算的软件

并行软件也有区别：

  • 内存共享系统上，一个进程 fork 出多个线程
  • 分布式系统上，需要多个进程

SPMD: single program multiple data，MPI 和 CUDA 都是用的都是这种。

解决并行软件的不一致性：给数据加锁

SPMD 的写法：

1
2
3
4
5
6
7
8
9
10
char message [ 1 0 0 ] ;
. . .
my_rank = Get_rank ( ) ;
if ( my_rank == 1) {
     sprintf ( message , "Greetings from process 1" ) ;
     Send ( message , MSG_CHAR , 100 , 0 ) ;
} else if ( my_rank == 0) {
     Receive ( message , MSG_CHAR , 100 , 1 ) ;
     printf ( "Process 0 > Received: %s\n" , message ) ;
}

输入输出

Google 翻译 yyds

当我们的并行程序需要进行 I/O 时，做出这些假设并遵循这些规则：
在分布式内存程序中，仅进程0将访问stdin。 在共享内存程序中，只有主线程或线程 0 会访问 stdin。
在分布式内存和共享内存程序中，所有进程/线程都可以访问 stdout 和 stderr。
然而，由于输出到 stdout 的顺序不确定，在大多数情况下，除了调试输出之外，只有一个进程/线程将用于所有输出到 stdout。
调试输出应始终包括生成输出的进程/线程的等级或 ID。
只有单个进程/线程会尝试访问除 stdin、stdout 或 stderr 之外的任何单个文件。 因此，例如，每个进程/线程都可以打开自己的私有文件进行读取或写入，但没有两个进程/线程会打开同一个文件。

3 Parallel Program Design

Foster 四步走

注意这四步，是设计算法的过程的四步，而不是并行算法的先后步骤。

  • Partitioning：分块
  • Communication：通信
  • Agglomeration：组合
  • Mapping：映射
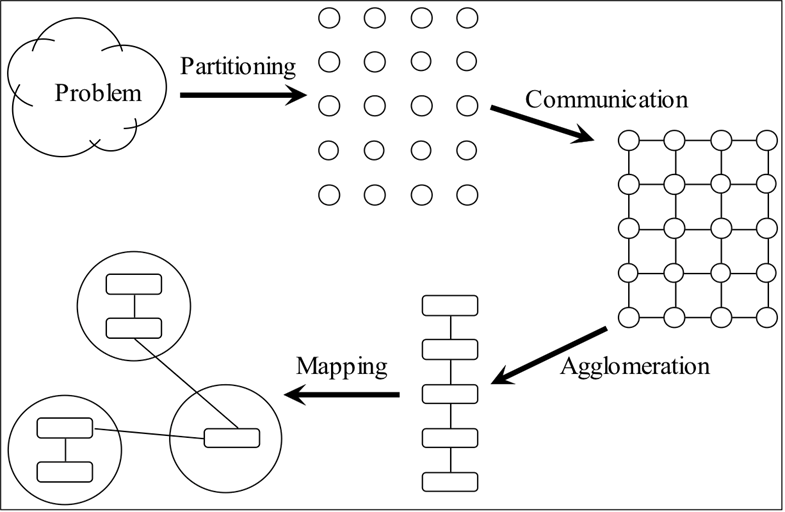
Foster’s Design Methodology
Foster’s Design Methodology

分块

Domain vs. Functional Decomposition

其实就是数据并行 vs. 任务并行

通信

通信方法可以分为局部通信和邻居通信

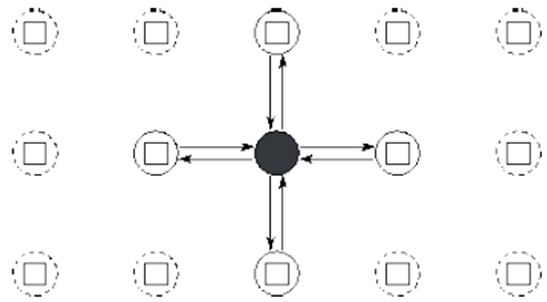
Local communication
Local communication
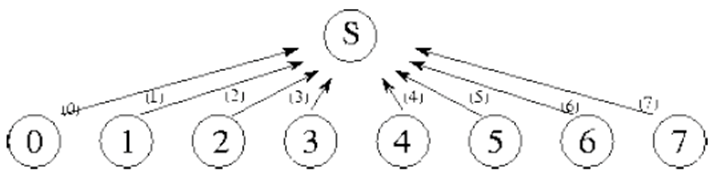
Global communication
Global communication

例子：对求和问题进行分治，只需要 logN 步

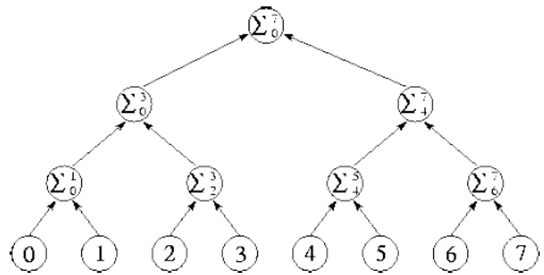
分治求和问题
分治求和问题

通信方法也可以分为结构化通信（通信网络有一定结构）和非结构化通信（通信网络可能是任意图）。

如果通信网络还在变化，负载均衡算法就必须频繁地更新。

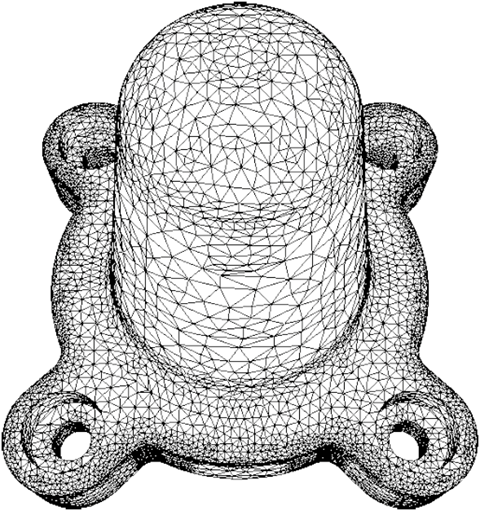
Unstructured communication
Unstructured communication

聚合

聚合可以减少通信成本：任务的通信需求与其操作的子域的表面成正比，而计算需求与子域的体积成正比。有时我们可以权衡复制计算以减少通信需求和/或执行时间。

映射

映射：将任务映射到处理器上。

目标：最大化处理器利用（即负载均衡） & 最小化处理器间通信（即需要通信的进程可以映射到同一处理器）

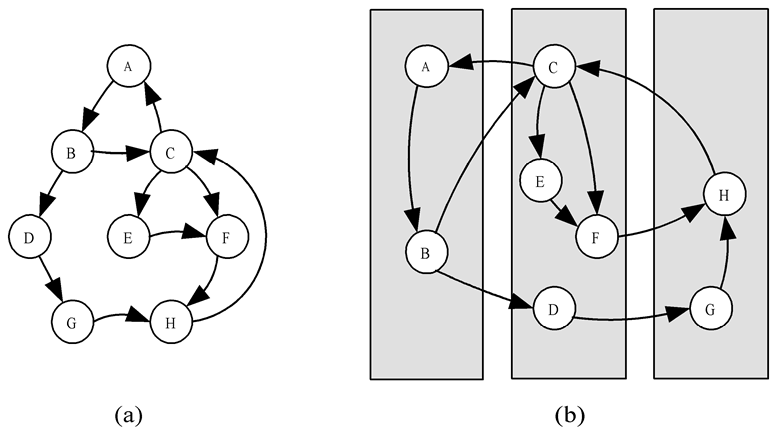
奇奇怪怪的图的一种映射方法
奇奇怪怪的图的一种映射方法

不同情况下映射策略：略。

Agglomeration 例题
Agglomeration 例题

公式：

  • $\chi$：更新一个元素的时间
  • $\lambda$：一个元素通信的时间
  • $n$：结点数
  • $m$：需要的迭代次数
  • $p$：处理器数

有一下结论：

  • 串行执行时间：$m(n-1)\chi$
  • 并行执行时间：$m\lceil(n-1)/p\rceil+2\lambda$

有点不懂。是在这个问题下的时间公式吗？

4 Performance

性能指标：运行时间、加速比、效率、可扩展性等

加速比和效率指标

$$S_p = \frac{T_s}{T_p}$$

  • $T_s$：串行时间
  • $T_p$：$p$ 个进程时的并行时间（按最长时间的进程计算）
  • $S_p$ or $\psi(n, p)$：$p$ 个进程时的加速比 (Speedup)

加速比是速度的正比，是时间的反比

$$\psi(n, p) \leq \frac{\sigma(n)+\varphi(n)}{\sigma(n)+\varphi(n) / p+\kappa(n, p)}$$

好的加速比：（相较进程数）线性加速、亚线性加速、超线性加速

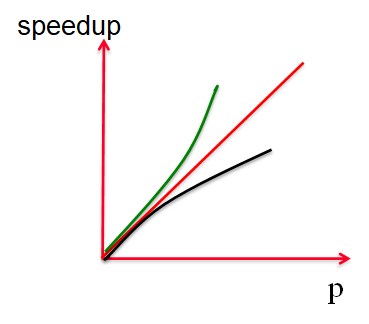
好的加速比
好的加速比

超线性加速出现在：多级内存、缓存影响、DFS 遍历树算法等。

$$\psi(n, p) \leq \frac{\sigma(n)+\varphi(n)}{\sigma(n)+\varphi(n) / p+\kappa(n, p)}$$

  • $\sigma(n)$：不能被并行执行的的串行时间
  • $\varphi(n)$：可以被并行执行的串行时间
  • $\kappa(n, p)$：并行执行带来的通信时间

比较显然，公式的意思是：并行算法的时间为：串行时间+并行部分/p+通行时间

这个公式一定要记住，后面的推导都是基于这个公式！

$$E_p=\frac{S_p}{p}$$

  • $E_p$ or $\varepsilon(n, p)$：效率

线性加速比程序的效率为 100%。

将 $S_p$ 代入即有：

$$\varepsilon(n, p) \leq \frac{\sigma(n)+\varphi(n)}{p\sigma(n)+\varphi(n)+p\kappa(n, p)}$$

可以推出 $0 \leq \varepsilon(n, p) \leq 1$。

Amdahl 定律

Amdahl 定律和 Gustafson-Barsis 定律都把通信成本放缩掉了。两个求的都是加速比，但是注意条件不一样（一个是 $f$ 一个是 $s$）

$$\psi(n, p) \leq \frac{\sigma(n)+\varphi(n)}{\sigma(n)+\varphi(n) / p+\kappa(n, p)}$$

令 $f$ 为串行部分占比（占改进之前的比），即 $f=\frac{\sigma(n)}{\sigma(n)+\varphi(n)}$，有：

$$\psi \leq \frac{1}{f+(1-f)/p}$$

加速比不大于“串行占比+p倍并行占比”的反比

例题：95% of a program’s execution time occurs inside a loop that can be executed in parallel. What is the maximum speedup we should expect from a parallel version of the program executing on 8 CPUs?

注意题目说的是串行在改进前需要执行 5% 的时间，这就符合 Amdahl 的条件。答案是 5.9。

Gustafson-Barsis 定律

令 $s$ 为串行部分占比（占改进之后的比），即 $s = \frac{\sigma(n)}{\sigma(n)+\varphi(n)/p}$，有：

$$\psi \leq p + (1-p)s$$

可以看到，如果 $s$ 小，$\psi \approx p$，并行效率很好。

例题：An application running on 10 processors spends 3% of its time in serial code. What is the scaled speedup of the application?

注意题目说的是串行代码在改进后需要执行 3% 的时间，这就符合 Gustafson-Barsis 的条件。答案是 9.73。

Karp-Flatt Metric 指标

Amdahl 和 Gustafson-Barsis 都忽略了通信成本，会高估放大比。Karp-Flatt 从另一个角度来进行分析。

但是这个公式起手就很怪异。

令$e = \frac{\sigma(n) + \kappa(n,p)}{\sigma(n)+\varphi(n)}$

串行时间 + 通信时间 / 串行时间 + 可并行的时间？

能够推出

$$e = \frac{1/\psi - 1/p}{1 - 1/p}$$

这个公式很奇怪，结合例题我大概看懂了：

结论 1：注意到 $n$ 一定的情况下，串行时间、可并行的时间 是恒定的，所以 $e$ 和 通信时间 的增长趋势是一样的。
即，在不同的 $p$ 下，如果 $e$ 恒定，说明通信时间恒定；$e$ 稳定增长，说明通信时间也稳定增长。

结论 2：随 $p$ 的增大，$e$ 不能先增大后减小（只能一直增大/不变或一直减小/不变：一直增大是次线性加速比，而一直减小就是超线性加速比）

例 1：

$p$ 2 3 4 5 6 7 8
$\psi$ 1.8 2.5 3.1 3.6 4.0 4.4 4.7
计算可得 $e$ 0.1 0.1 0.1 0.1 0.1 0.1 0.1

为什么 8 核的加速比只有 4.7？注意到 $e$ 不随 $p$ 变化，说明问题不是通信成本，是串行代码耗时太高。

例 2：

$p$ 2 3 4 5 6 7 8
$\psi$ 1.9 2.6 3.2 3.7 4.1 4.5 4.7
计算可得 $e$ 0.07 0.075 0.08 0.085 0.09 0.095 0.1

为什么 8 核的加速比只有 4.7？注意到 $e$ 不随 $p$ 变化，说明问题不是通信成本，是串行代码耗时太高。

例 3：

$p$ 4 8 12
$\psi$ 3.9 6.5 ？

? 处能否为 10？

假设 ?=10，算得 $e$ 先增大后减小，不可能。

等效率

不会，看 PPT

可扩展性

不会，看 PPT

5 Message-Passing Programming

MPI 常用函数

1
2
3
4
5
6
7
8
9
10
11
//First MPI function called by each process
MPI_Init (&argc, &argv);

// First argument is communicator
// Number of processes returned through second argument
MPI_Comm_size (MPI_COMM_WORLD, &p);
// Process rank (in range 0, 1, …, p-1) returned through second argument
MPI_Comm_rank (MPI_COMM_WORLD, &id);

// Call after all other MPI library calls
MPI_Finalize();
1
2
3
4
5
6
7
8
9
10
11
// reduce 操作
int MPI_Reduce (
    void *operand,      /* addr of 1st reduction element */
    void *result,       /* addr of 1st reduction result, only root get result */
    int count,          /* reductions to perform */
    MPI_Datatype type,  /* type of elements */
    MPI_Op operator,    /* reduction operator */
    int root,           /* process getting result(s) */
    MPI_Comm comm       /* communicator */
)
MPI_Reduce (&count, &global_count, MPI_INT, 0, MPI_COMM_WORLD);
1
2
3
4
5
6
7
8
// Benchmarking the Program
double elapsed_time;
MPI_Init (&argc, &argv);
MPI_Barrier (MPI_COMM_WORLD);
elapsed_time = - MPI_Wtime();
// ...
MPI_Reduce (…);
elapsed_time += MPI_Wtime();

附 MPICH 中文教程

https://scc.ustc.edu.cn/zlsc/cxyy/200910/MPICH/

6 The Sieve of Eratosthenes

因为这部分做了实验，所以不多说算法原理了。

1
2
3
4
5
6
7
int MPI_Bcast (
    void *buffer,           /* Addr of 1st element */
    int count,              /* # elements to broadcast */
    MPI_Datatype datatype,  /* Type of elements */
    int root,               /* ID of root process */
    MPI_Comm comm)          /* Communicator */
MPI_Bcast (&k, 1, MPI_INT, 0, MPI_COMM_WORLD);

分块算法

这个问题需要按数据分块。可以使用循环分配，可以按块分配。

使用循环分配，

$$my\_first\_i = i * \lfloor\frac{n}{p}\rfloor + \min(i,r)\\
my\_last\_i = (i+1)* \lfloor\frac{n}{p}\rfloor + \min(i+1,r) - 1 \\
count= \min(\lfloor \frac{j}{\lfloor n / p \rfloor+1}\rfloor, \lfloor \frac{j-r}{\lfloor n / p \rfloor}\rfloor)
$$

使用按块分配，就是第一章的习题中提到的：

$$my\_first\_i = \lfloor\frac{i*n}{p}\rfloor\\
my\_last\_i = \lfloor\frac{(i+1)*n}{p}\rfloor - 1 \\
count=\lfloor \frac{p(j+1)-1}{n}\rfloor
$$

两种算法都可以，后面一种表达式更简单，所以选择这一种。

算法性能分析

时间复杂度
时间复杂度

7 Floyd’s Algorithm

Floyd 算法伪代码：

1
2
3
4
5
6
7
for k = 0 to n-1
    for i = 0 to n-1
        for j = 0 to n-1
            a[i,j] = min (a[i,j], a[i,k] + a[k,j])
        endfor
    endfor
endfor

分块

把矩阵 A 的每个元素视为一个任务，分解成 $n^2$ 个任务。

通信

通信
通信

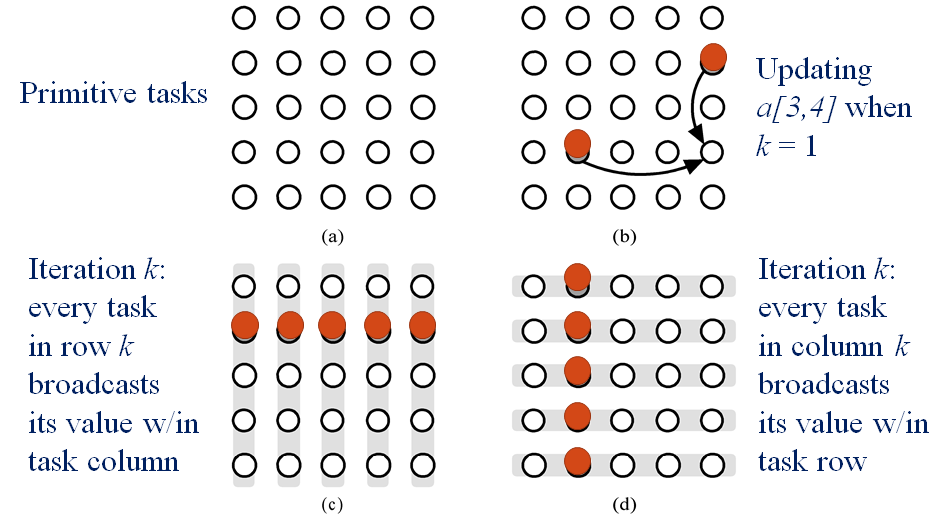
聚合和映射

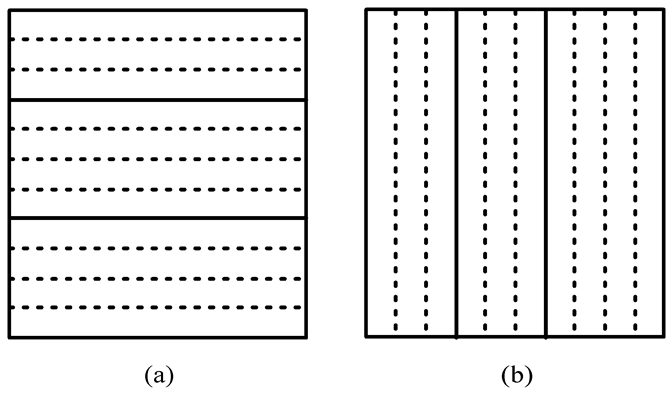
按行或者按列聚合
按行或者按列聚合

按行或者按列聚合。最后选择按行聚合，在读文件的时候会容易的多。

点对点通信

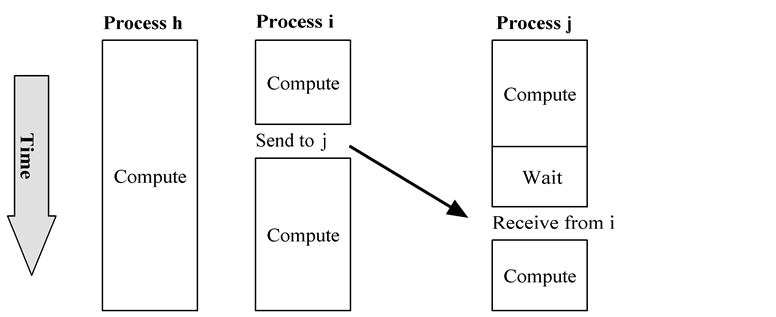
点对点通信
点对点通信
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
int MPI_Send (
    void         *message,
    int           count,
    MPI_Datatype  datatype,
    int           dest,
    int           tag,
    MPI_Comm      comm
)

int MPI_Recv (
    void         *message,
    int           count,
    MPI_Datatype  datatype,
    int           source,
    int           tag,
    MPI_Comm      comm,
    MPI_Status   *status
)

Send 和 Recv 需要约定相同的 tag，以及对方的 id (作为自己的 source/dest)。

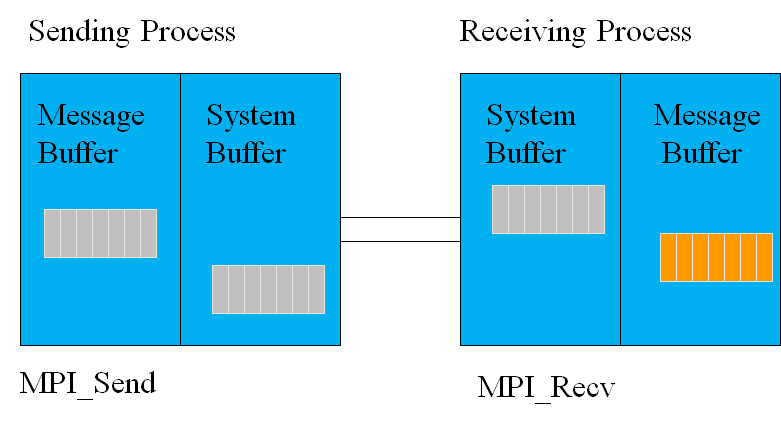
send/recv 原理
send/recv 原理
  • MPI_Send 函数会一直阻塞直至 message_buffer 空了。
  • MPI_Recv 函数会一直阻塞直至收到消息。

这就很容易造成死锁。

死锁

1
2
3
4
5
6
7
8
9
if (id == 0) {
    MPI_Recv (&b,...);
    MPI_Send (&a,...);
   c = (a + b)/2.0; 
} else if (id == 1) {
    MPI_Recv (&a,...);
    MPI_Send (&b,...);
   c = (a + b)/2.0; 
}

Process 0 blocks waiting for message from 1, but 1 blocks waiting for a message from 0.
Deadlock!

1
2
3
4
5
6
7
8
9
if (id ==0) {
    MPI_Send(&a, ... 1,MPI_COMM_WORLD);
    MPI_Recv(&b, ... 1, MPI_COMM_WORLD,&status);
    c = (a+b)/2.0; 
}else if (id ==1) {
    MPI_Send(&a, ... 0,MPI_COMM_WORLD);
    MPI_Recv(&b, ... 0, MPI_COMM_WORLD,&status);
    c = (a+b)/2.0;
}

Both processes send before they try to receive, but they still deadlock. Why?
The tags are wrong. Process 0 is trying to receive a tag of 1, but Process 1 is sending a tag of 0.

Ssend

依赖 buffer 的 MPI_send 是不安全的，因为 MPI 标准允许 MPI_Send 可以提供/不提供 buffer。

两种问题可能会出问题：

  1. 双方都是先发后收，并且发的数据都很大
  2. 生产者/消费者问题，且生产者生产的比消费者块

MPI 标准定义了 MPI_Ssend，保证发送会被阻塞（s 表 synchronous）。

SendRecv

如果需要同时发送接收，可以通过代码逻辑使大家按照某种顺序，避免死锁，但也可以使用 MPI_SendRecv 同时发送和接收，中间的调度由 MPI 实现。

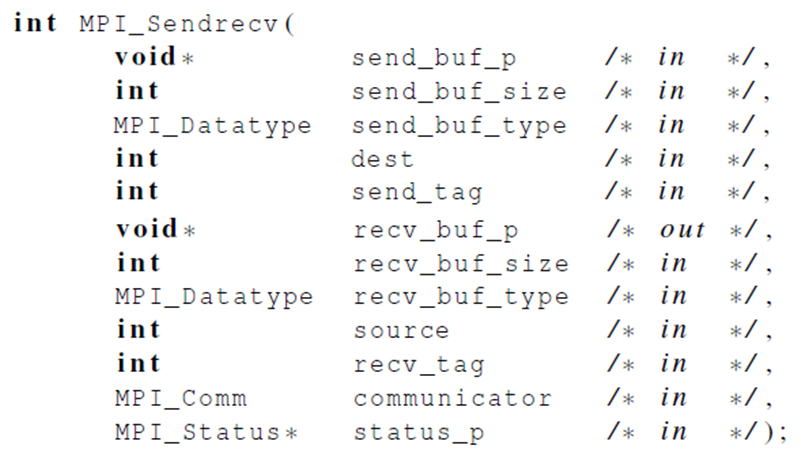
MPI_SendRecv
MPI_SendRecv

并行 Floyd 算法

核心部分
核心部分
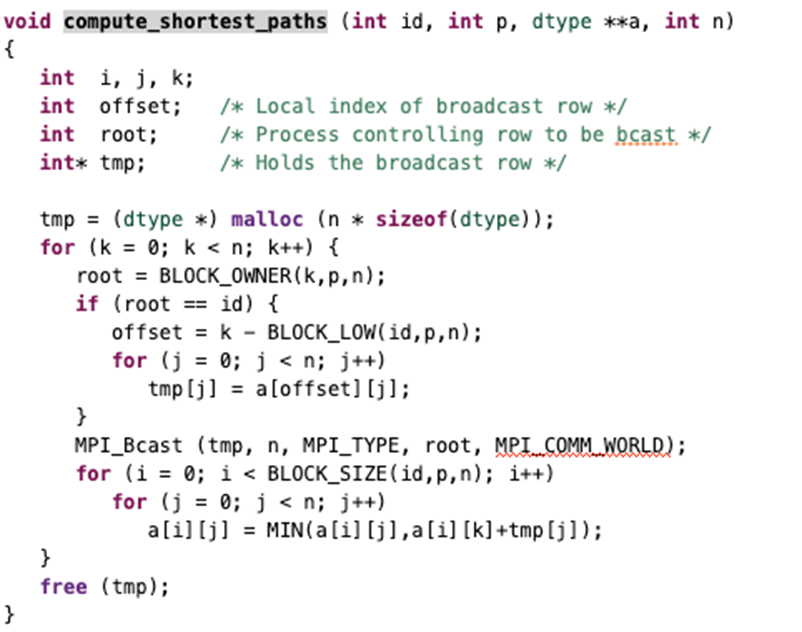
  • 计算时间复杂度：$\Theta(n^3/p)$
  • 通信时间复杂度：$n^2 \log p$
  • 执行时间（其中 $\beta$ 是显存带宽，其他变量见第三章）：

$$n \lceil n / p \rceil n \chi +
n \lceil \log p \rceil (\lambda + 4n / \beta)$$

CUDA 部分

结构

  • Thread – Register
  • Warp
  • Block – 对应一个 Streming Multiprocessors，Shared Memory
  • Grid – 对应一个 Kernel
  • Device – Global Memory

代码思路

用 Block 处理二维图像：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
__global__ void PictureKernel(float* d_Pin, float* d_Pout, int height, int width)
{
  int Row = blockIdx.y*blockDim.y + threadIdx.y;
  int Col = blockIdx.x*blockDim.x + threadIdx.x;
  if ((Row < height) && (Col < width)) {
    d_Pout[Row*width+Col] = 2.0*d_Pin[Row*width+Col];
  }
}

int main()
{
  dim3 DimGrid((n-1)/16 + 1, (m-1)/16+1, 1);
  dim3 DimBlock(16, 16, 1);
  PictureKernel<<<DimGrid,DimBlock>>>(d_Pin, d_Pout, m, n);
}

Block 大小

For Matrix Multiplication using multiple blocks, should I use 8X8, 16X16 or 32X32 blocks for Fermi?

  • For 8X8, we have 64 threads per Block. Since each SM can take up to 1536 threads, which translates to 24 Blocks. However, each SM can only take up to 8 Blocks, only 512 threads will go into each SM!
  • For 16X16, we have 256 threads per Block. Since each SM can take up to 1536 threads, it can take up to 6 Blocks and achieve full capacity unless other resource considerations overrule.
  • For 32X32, we would have 1024 threads per Block. Only one block can fit into an SM for Fermi. Using only 2/3 of the thread capacity of an SM.

CGMA

CGMA = 从全局内存中取一个数，多少次运算用到了这个数

CGMA 越大越好

Shared Memory And Threading

Shared Memory And Threading
Shared Memory And Threading

OpenACC 部分

GPU 占用率

GPU Occupancy is:

  • How much parallelism is running / How much parallelism the hardware could run
  • 100% occupancy is not required for, nor does it guarantee best performance.
  • Less than 50% occupancy is often a red flag